Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.6 - Ex. 27

Calcular a área da região sob o gráfico y = - (1)/(x^2 (x - 5)) , de x = 1 até x = 4 .

Passo 1

A área pedida é a da figura aqui:

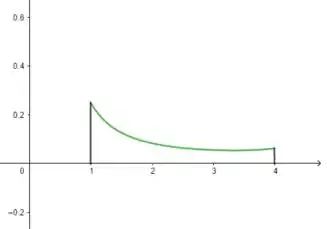
Passo 2

Pra calcular a área aqui é só a gente resolver a integral:

int_1^4 - (1)/(x^2 (x - 5)) d x

Aqui a gente tem um termo quadrático e um termo linear, então a gente usa frações parciais assim:

(1)/(x^2 (x - 5)) = (A)/(x) + (B)/(x^2) + (C)/(x - 5)

Aí a gente tem que achar A , B e C .

Passo 3

Vai ficar assim:

(1)/(x^2 (x - 5)) = (A x ( x - 5 ))/(x) + (B ( x - 5 ))/(x^2) + (C x^2)/(x - 5)

Cortamos os denominadores...

1 = A x (x - 2) + B (x - 5) + C x^2

1 = A x^2 - 2 A x + B x - 5 B + C x^2

1 = x^2 (A + C) + x (- 2 A + B) - 5 B

Pra ser igual, a gente precisa que:

{[[A + C = 0],[- 2 A + B = 0],[- 5 B = 1]])

Daqui a gente acha B = - (1)/(5) ; A = - (1)/(25) ; C = (1)/(25) .

Passo 4

Vamos remontar a integral:

(1)/(x^2 (x - 5)) = - (1)/(25 x) - (1)/(5 x^2) + (1)/(25 (x - 5))

- int_1^4 - (1)/(25 x) - (1)/(5 x^2) + (1)/(25 (x - 5)) d x

- [- (1)/(25) int_1^4 (1)/(x) d x - (1)/(5) int_1^4 (1)/(x^2) d x + (1)/(25) int_1^4 (1)/(x - 5) d x]

- [- (1)/(25) ln x + (1)/(5 x) + (1)/(25) ln |x - 5|]_1^4

+ (1)/(25) ln 4 - (1)/(20) - (1)/(25) ln |- 1| - (1)/(25) ln 1 + (1)/(5) + (1)/(25) ln | - 4 |

(2)/(25) ln 4 + (3)/(20) u . a

Prontinho! Essa é a área pedida😊

Resposta

(2)/(25) ln 4 + (3)/(20) u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral.int (d x)/(x^2 - 6 x - 7)
Calcule a integral.int (5 x - 5)/(3 x^2 - 8 x - 3) d x
Calcule a integral.int (3 x^2 - 10)/(x^2 - 4 x + 4) d x
Calcule a integral.int (x^5 - 4 x^3 + 1)/(x^3 - 4 x) d x
Calcule a integral.int (2 x^2 + 3)/(x (x - 1)^2) d x