Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 19
Calcular as integrais curvilíneas.
, onde é a semicircunferência da Figura 9.18.
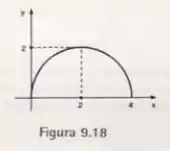
Passo 1
Vamos parametrizar a região, como é um semicírculo, a gente parametriza com coordenadas polares.
Fica assim:
O intervalo de vai ser de , já que é metade de uma circunferência.
Agora a gente deriva essa parametrização e faz a norma, que é o nosso ...
A norma agora:
Beleza, agora é só jogar isso tudo na integral de linha e calcular...
Passo 2
A integral fica:
Prontinho😉
Resposta
Exercícios de Livros Relacionados
O fio mostrado na Figura 9.22 conduz uma corrente i . Determinar a intensidade do campo magnético B → no centro de C do semicírculo, produzido:Por um dos segmentos de reta de comprimento l .
O fio mostrado na Figura 9.22 conduz uma corrente i . Determinar a intensidade do campo magnético B → no centro de C do semicírculo, produzido:b) pelo fio todo.
Um segmento retilíneo de fio, de comprimento l , conduz uma corrente i . Mostrar que a intensidade do campo magnético B → associada a esse segmento, a uma distância R , tomada sobre a mediatriz é dada
Uma espira quadrada de lado a conduz uma corrente i . Mostrar que a intensidade do campo magnético B → , no centro, é dada por 8 2 k i a
Calcule ∫ γ x 2 + y 2 d s Onde γ t = ( t , t ) , - 1 ≤ t ≤ 1