Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 30

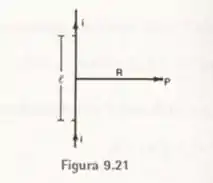
Um segmento retilíneo de fio, de comprimento l , conduz uma corrente i . Mostrar que a intensidade do campo magnético B → associada a esse segmento, a uma distância R , tomada sobre a mediatriz é dada por:

B =   2 k i l R l 2 + 4 R 2 1 2

Passo 1

Vamos considerar o eixo vertical sendo o z e daí podemos dizer que ele está indo de - l 2 a l 2 .

Considerando o eixo onde está o ponto P sendo o eixo x , podemos dizer que ele está na posição ( R , 0 ) .

E daí, a distância de um ponto do eixo z onde está a corrente até o ponto é dada por:

r = R 2 + z 2

(lembra que a gente usa o quadrado da distância)

Aí nós montamos a integral:

∫ - l 2 l 2 d z z ^ × R - z R 2 + z 2 i   R 2 + z 2  

Passo 2

Vamos arrumar essa integral agora:

= ∫ - l 2 l 2 d z R 2 + z 2 3 2

Integrando isso aqui dá:

= z R 2 R 2 + z 2 - l 2 l 2

l 2 R 2 R 2 + l 2 4 + l 2 R 2 R 2 + l 2 4

= l R 2 4 R 2 + l 2 4

= 2 l R 2 4 R 2 + l 2

Passo 3

Voltando isso para o campo magnético agora...

B = k i R ∙ 2 l R 2 4 R 2 + l 2

B = 2 k i l R 4 R 2 + l 2

Do jeitinho que era pra ser😊

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espira quadrada de lado a conduz uma corrente i . Mostrar que a intensidade do campo magnético B → , no centro, é dada por 8 2 k i a
Calcule ∫ γ x 2 + y 2 d s Onde γ t = ( t , t ) , - 1 ≤ t ≤ 1
Calcule ∫ γ x y z d s Onde γ t = cos ⁡ t ,s e nt , t , 0 ≤ t ≤ 2 π
Calcule ∫ γ 2 x y + y 2 d s Onde γ t = ( t + 1 , t - 1 ) , 0 ≤ t ≤ 1