Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.5 - Ex. 13

Calcular a integral tripla dada sobre a região indicada

∫ ∫ ∫ T z d V

Onde T é a região do primeiro octante limitada por   z 2 + y 2 = 2   ,   y = 2 x ,   x = 0 .

Passo 1

Lembra que na integral tripla o d V   é a mesma coisa que d x d y d z , então sabemos que as integrais triplas podem ser calculadas de forma análoga às integrais duplas, por meio de integrações sucessivas.

Para calcular as integrais duplas precisávamos ter noção da região de integração, aqui em integrais triplas vamos precisar da mesma noção.

Passo 2

Nossa superfície T é delimitada por:

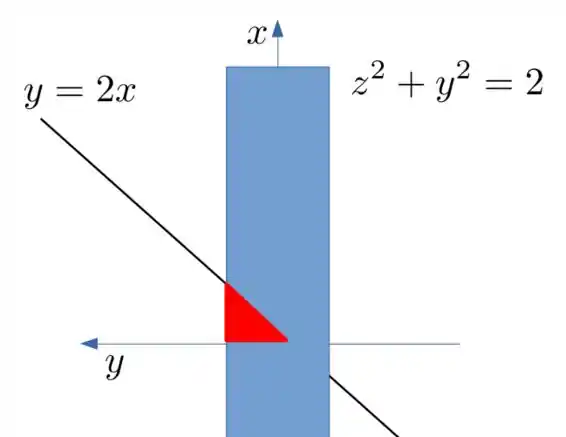
A nossa região é um cilindro cortado pelo plano y = 2 x e que está no primeiro octante. Só de estar no primeiro octante já sabemos que

0 < x ,   0 < y ,   0 < z

Já a coordenada y é no máximo o raio do cilindro. Isso significa que a coordenada x vai de 0 até x = y 2 .

0 ≤ x ≤ y 2

Pelo meu desenho aqui (ou melhor, obra de arte haha) a coordenada y tá dentro do cilindro e acima do plano y = 2 x , então

0 ≤ y ≤ 2

E a coordenada z tem que ser maior que 0 e estar dentro do cilindro

0 ≤ z ≤ 2 - y 2

Passo 3

Agora vamos deixar nossa integral na forma com as três variáveis e depois colocá-la na forma iterada :

∫ ∫ ∫ T z d V = ∫ 0 2 d y ∫ 0 y / 2 d x ∫ 0 2 - y 2 z d z

Aí agora é só calcular!

= ∫ 0 2 d y ∫ 0 y 2 d x   z 2 2 0 2 - y 2

= ∫ 0 2 d y ∫ 0 y 2 2 - y 2 2 d x

= ∫ 0 2 d y 2 - y 2 2 x 0 y 2

= ∫ 0 2 2 - y 2 2 y 2 d y

= ∫ 0 2 2 y - y 3 4 d y

= 1 4 ∫ 0 2 2 y - y 3 d y

= 1 4 y 2 - y 4 4 0 2

= 1 4 2 - 4 4

= 1 4 2 - 1

= 1 4

Show! Conseguimos :D

Resposta

1 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do sólido dado. Abaixo da superfície z = x 2 y e acima do triângulo no plano x y com vértices 1,0 ,2,1e4,0 .
Determine o volume do sólido dado. Uma das cunhas obtidas pelo corte do cilindro x 2 + 9 y 2 = a 2 pelos planos z = 0 e z = m x .
Uma luminária tem três lâmpadas, cada uma com vida média de 800h o r a s . Se modelarmos a probabilidade de falha das lâmpadas por uma função densidade exponencial com média 800 , determine a probabil
Utilize a transformação x = u 2 , y = v 2 , z = w 2 para determinar o volume da região limitada pela superfície x + y + z = 1 e pelos planos coordenados.
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro y = x 2 e pelos planos z = 0 e y + z = 1