Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 22

Calcular a massa de arame cujo formato é definido pela interseção do plano 2 x + y + z = 4 com os planos coordenados, se a densidade do arame em um ponto x ,   y , z é 2 x + 1 .

Passo 1

O arame vai ser definido pelos pontos em que o plano corta os eixos.

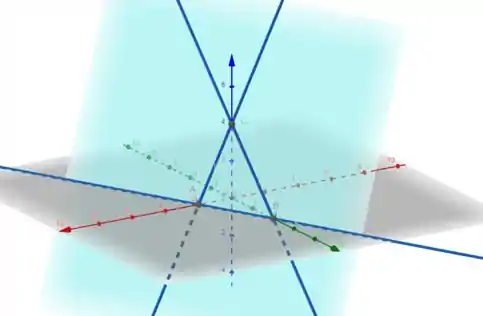
Vamos fazer a massa de cada reta, e depois somar.

Passo 2

Vamos começar pela reta que vai de A 2,0 , 0 a   B ( 0,4 , 0 ) .

Podemos parametrizar essa reta como:

r : x = 2 - 2 t y = 4 t z = 0 ,   t ∈ [ 0,1 ]

Aqui a gente faz norma do vetor, que será o nosso d s :

d s = - 2 2 + 4 2 = 20

Montando a integral da massa agora...

M = ∫ 0 1 2 2 - 2 t + 1 20 d t

= 20 ∫ 0 1 5 - 4 t   d t

= 20 5 t - 2 t 2 0 1

= 20 5 - 2

= 3 20

Essa é a massa da primeira reta.

Passo 3

Vamos agora pra reta que vai de B 0,4 , 0   a   C ( 0,0 , 4 ) . Podemos parametrizar como:

r : x = 0 y = 4 - 4 t z = 4 t ,   t ∈ [ 0,1 ]

A norma do vetor aqui é:

d s = 0 2 + - 4 2 + 4 2 = 32

A massa então...

M = ∫ 0 1 2 0 + 1 32 d t

= ∫ 0 1 32 d t

= 32

Pronto! Dessa já foi também.

Passo 4

Vamos para a última reta, que sai de C 0,0 , 4 para A ( 2,0 , 0 ) . Parametrizamos...

r : x = 2 t y = 0 z = 4 - 4 t ,   t ∈ [ 0,1 ]

Fazemos a norma do vetor, que é o d s :

d s = 2 2 + 0 2 + - 4 2

d s = 20

Montamos a integral da massa agora:

∫ 0 1 2 2 t + 1 20 d t

= 20 ∫ 0 1 4 t + 1   d t

= 20 2 t 2 + t 0 1

= 3 20

Isso aí!

Passo 5

Somamos as três massas encontradas agora e encontramos a massa do arame...

M = 3 20 + 32 + 3 20

M = 6 20 + 32

Prontinho😉

Resposta

M = 6 20 + 32

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Fio helicoidal com densidade constante - Encontre a massa e o centro de massa de um fio de densidade constante δ que está ao longo da hélice r t = 2 sen ⁡ t i + 2 cos ⁡ t j + 3 t k , 0 ≤ t ≤ 2 π .
Fio com densidade constante - Um fio de densidade constante δ = 1 está ao longo da curva r t = e t cos ⁡ t i + e t sen ⁡ t j + e t k ,0 ≤ t ≤ ln ⁡ 2 . Encontre z e I z .
Fio com densidades diferentes - Encontre a massa de um fio fino ao longo da curva r t = 2 t i + 2 t j + 4 - t 2 k ,0 ≤ t ≤ 1 , se a densidade em t for (a) δ = 3 t e (b) δ = 1 .
Inércia e centro de massa de uma casca - Encontre I z e o centro de massa de uma casca fina de densidade δ x , y , z = z cortada a partir da porção superior da esfera x 2 + y 2 + z 2 = 25 pelo plano z
Momento de inércia de um cubo - Encontre o momento de inércia em relação ao eixo z da superfície do cubo cortado do primeiro octante pelos planos x = 1, y = 1 e z = 1 se a densidade for δ = 1 .