Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 28

Calcular a massa de um fio delgado reto de 2 m   de comprimento se a densidade em cada ponto é proporcional à distância desse ponto à extremidade mais próxima.

Passo 1

Vamos considerar o fio assim:

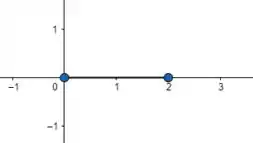
A gente pode parametrizar esse fio como:

x = t y = 0   ,     t ∈ [ 0 , 2 ]

E aí a derivada é 1 ,   0 e a norma é 1 .

A densidade vai ser proporcional a distância de um ponto à extremidade, podemos considerar então que no intervalo de 0   a   1 , a distância vai ser o valor do ponto (pois estará mais próximo do ponto inicial) , e de 1   a   2 será o comprimento total menos o valor do ponto. Ou seja:

ρ = k t ,   0,1

ρ = k ( 2 - t ) ,   [ 1,2 ]  

Passo 2

Vamos montar as integrais agora:

M 1 : ∫ 0 1 k t   1 d t

k t 2 2 0 1 = 1 2 k

E...

M 2 : ∫ 1 2 k 2 - t 1 d t

k 2 t - t 2 2 1 2

= k 4 - 2 - 2 + 1 2 = 1 2 k

Somamos as duas massas encontradas agora...

M = 1 2 k + 1 2 k = k   u . m

Resposta

k   u . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa e o centro de massa de um arame com formato da hélice x = t, y = cos ⁡ t, z = s e nt, 0 ≤ t ≤ 2 π, se a densidade em qualquer ponto for igual ao quadrado da sua distância do ponto à
(a) Escreva fórmulas semelhantes à Equação 4 para o centro de massa x C M ,y C M ,z C M de um arame fino com função densidade ρ x ,y ,z e forma da curva espacial C .(b) Determine o centro de massa de
Se um arame com densidade linear ρ x ,y está sobre uma curva plana C , seus momentos de inércia em relação aos eixos x e y são definidos por I x = ∫ C y 2ρ x ,y d s I y = ∫ C x 2ρ x ,y d s Determine o
Se um arame com densidade linear ρ x ,y ,z está sobre uma curva espacial C , seus momentos de inércia em relação aos eixos x , y e z são definidos por I x = ∫ C ( y 2 + z 2 ) ρ x ,y d s I y = ∫ C ( x
Fio com densidade variável - Encontre o centro de massa de um fio fino presente ao longo da curva r t = t i + 2 t j + 2 3 t 3 / 2 k ,0 ≤ t ≤ 2 , se a densidade em t for δ = 3 5 + t .