Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 29
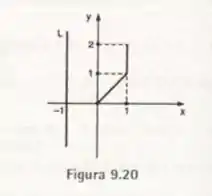
A figura 9.20 mostra um fio delgado e um eixo . Calcular o momento de inércia do fio em relação ao eixo , supondo a densidade constante.
Passo 1
Vamos ter que dividir a região aqui em duas. Uma que vai de e outra que vai de .
A reta de a gente pode parametrizar como:
Aí a derivada é e a norma .
Bom, nessa primeira reta, a distância de um ponto qualquer ao eixo é (veja que só tem variação em uma das coordenadas, pois o eixo é )
Vamos montar essa integral de momento de inércia de uma vez então, lembrando que a densidade é constante, vamos chamar de
Passo 2
O primeiro momento de inércia é:
Passo 3
Vamos para a outra reta agora, de . Uma parametrização para a reta é:
E aí a derivada disso é e a norma é .
A distância de um ponto dessa reta até o eixo é . Então montando a integral, a gente tem:
Somando os dois momentos de inércia encontrados, nós achamos:
Prontinho!