Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 33

Calcular

∫ ∫ S 2 z   d S  

Onde S é a parte do paraboloide   z   =   x ²   + y ² -   2 abaixo do plano xy

Passo 1

A região que queremos é essa aqui

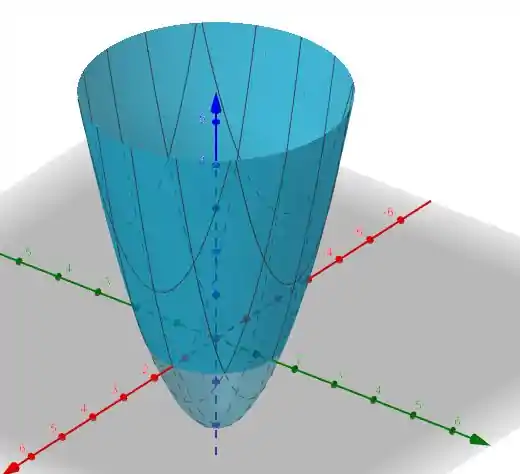
Abaixo do plano XY. Isso quer dizer que quando projetarmos no plano XY teremos um circulo

; )

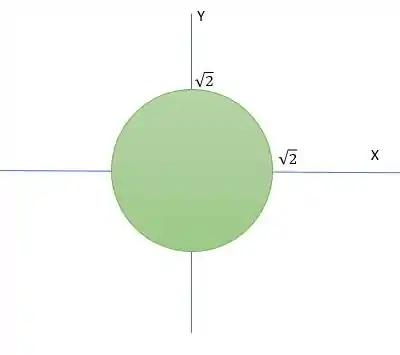
Para sabermos qual o raio do circulo é traquilo, temos a equação

z   =   x 2 + y 2 -   2

O circulo maior é quando z → 0

0   =   x 2 + y 2 -   2

x 2 + y 2 = 2 2

Passo 2

Agora temos que ter em mente que estaremos trabalhando com uma região circular, logo algum momento vamos precisar mudar de coordenas de cartesianas →   polares

Então beleza! Nossa integral vai ser nesse moldes abaixo

∫ ∫ S f   d S =   ∫ ∫ R f   x , y ,   z ( x , y )   1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Então ficamos com

∫ ∫ R 2 ( x ²   + y ² -   2 ) 1 + ∂ z ∂ y 2 + ∂ z ∂ x 2 d y d x

Vamos calcular as derivadas parciais de z, onde lembra que

z   =   x 2 + y 2 -   2

Logo

z x =   2 x

z y = 2 y

Vamos terminar nossa integração

∫ ∫ R 2 ( x ²   + y ² -   2 ) 1 + 2 x 2 + 2 y 2 d y d x

∫ ∫ R 2 ( x ²   + y ² -   2 ) 1 + 4 x 2 + y 2   d y d x

Passo 3

Agora é agora trocarmos as variáveis cartesiana → polar.

x 2 + y 2 = r 2

0 ≤ r ≤ 2

0 ≤ θ ≤ 2 π

Assim nossa integral fica assim

∫ 0 2 π ∫ 0 2 2 r 2 - 2   1 + 4 r ²   r d r d θ

Lembrando que temos que multiplicar pelo jacobiano porque estamos corrigindo o espaço. Agora podemos integrar primeiro por θ   porque nossa equação não é dependente dessa variável.

= 2 * 2 π ∫ 0 2 r 2 - 2   1 + 4 r ²   r d r  

= 4 π ∫ 0 2 r ² r 1 + 4 r 2   d r -   ∫ 0 2 2 r 1 + 4 r 2   d r    

EITA!!! Ficou estranho, certo? Relaxa! Pra resolver Vamos precisar fazer uma substituição aqui

1 + 4 r 2 = u

r 2 = u - 1 4    

8 r d r = d u

4 π ∫ 1 8 u - 1 4 u   d u -   ∫ 2 8 u   d u

=   4 π ∫ 1 32 u 3 / 2   d u - ∫ 1 32 u 1 / 2   d u -   ∫ 1 4 u 1 / 2   d u

= 4 π   1 32 * 2 5 u 5 2 - 1 32 * 2 3 u 3 2 - 1 4 * 2 3 u 3 2  

Vamos voltar agora de u → r

= 4 π   1 32 * 2 5 1 + 4 r 2 5 2 - 1 32 * 2 3 1 + 4 r 2 3 2 - 1 4 * 2 3 1 + 4 r 2 3 2   r =   0 2

= 4 π - 37 20

=   - 37 π 5

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ S 2 z   d S   = - 37 π 5  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja S a superfície que é fronteira da caixa delimitada pelos planos x = 0,x = 2,y = 0,y = 4,z = 0 e z = 6 . Aproxime ∫ ∫ Se - 0,1 x + y + zd S usando uma soma de Riemann, como na Definição 1 , tomand
Determine a área da superfície.A parte do plano 3 x + 2 y + z = 6 que está no primeiro octante.
Determine a área da superfície.A parte do paraboloide hiperbólico z = y 2 - x 2 que está entre os cilindros x 2 + y 2 = 1 e x 2 + y 2 = 4
Determine a área da superfície.A parte do plano 2 x + 5 y + z = 10 que está dentro do cilindro x 2 + y 2 = 9 .
Determine a área da superfície.A superfície z = (2)/(3) (x^((3)/(2)) + y^((3)/(2))) , 0 = x = 1 , 0 = y = 1 .