Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 34

Calcular

∫ ∫ S x   d S  

Onde S é a superfície plana z - x = 2   recortada pela esfera x 2 +   y 2 + z 2 = 2 z

Passo 1

Essa questão é meio complicada. Se piscarmos ficamos perdidos.

Primeiro, temos uma região mista. Nossa superfície é o PLANO z - x = 2 . Precisamos lembrar disso.

Segundo, temos o plano cortado pela esfera, logo teremos uma região circular ( sendo mais preciso uma elipse )

Terceiro, vamos precisar trocar as variáveis para fazer a integração. Cartesiana →     Polar

Vamos então descobrir que região é essa que temos

z - x = 2

x 2 +   y 2 + z 2 = 2 z

Vamos manipular um pouco essa equações para deixar claro o que queremos – Eliminar a variável Z

z = x + 2

x 2 + y 2 + z 2 - 2 z = 0

Completando quadrado temos que

x 2 + y 2 + z - 1 2 = 1

Agora vamos substituir a primeira equação na segunda

x 2 + y 2 + ( x + 2 ) - 1 2 = 1

x 2 + y 2 + x + 1 2 = 1

Organizando a equação de cima temos

2 x 2 + x + y 2 = 0

Pode não parecer, mas essa equação é de uma elipse. Mas para ficar evidente precisaremos completar quadrados. Assim depois de algumas manipulações temos

4 x + 1 2 2 + 2 y 2 = 1

Agora sim fica mais claro a região que temos. Vou plotar o gráfico dela para gente ver

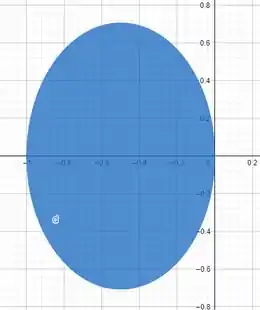
Passo 2

Primeira coisa a dizer. Essa região é muito ruim de integrar, porque ela está descentralizada dos eixos. Isso quer dizer que quando mudarmos para polar o nosso r   sera uma função do ângulo r ( θ ) , ou seja, você vai pedir arrego no meio do exercício, porque ele ficaria imenso.

Então tenho uma super dica do meu professor de calculo 3. Vamos fazer uma mudança de espaço vamos sair dessa região cartesiana para uma cartesina*

C → C *

Onde nessa nossa região cartesiana a nossa região esteja centralizada. Faremos assim

y * = y

x * = x + 1 2

O melhor desse tipo de transformação é que o Jacobiano – A distorção espacial é 1. Porque não estamos distorcendo o espaço, apenas transladando. Então nossa integral fica

∫ ∫ S x * - 1 2   d S  

E agora sim nossa elipse fica centralizada

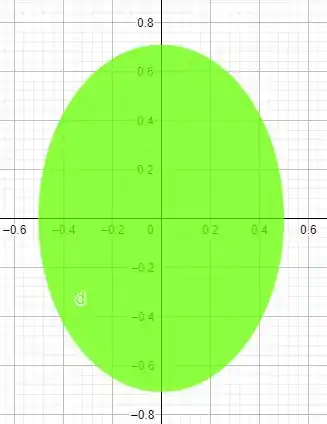
Agora que sabemos que mudamos já de C → C * , não vou mais por x * nem y * . Blz ? ; )

Passo 3

Agora que vamos fazer a mudança de variável para Polar eliptica

x = a r c o s θ

y = b r c o s θ

Onde a equação da elipse é

x a 2 + y b 2 = 1

OU seja a nossa equação fica

4 x + 1 2 2 + 2 y 2 = 1

Onde

a = 1 4

b = 1 2

E o jacobiano é

J = a b r

Vamos integrar agora

∫ ∫ S x * - 1 2   d S   =   ∫ 0 2 π ∫ 0 1 r c o s θ - 1 2   1 4 1 2   r d r d θ

Dica : Quando integramos seno ou cosseno entre [ 0,2 π ] o resultado é 0. Logo podemos primeiro integrar em relação a θ que já eliminamos o termo r c o s θ

- 2 π ∫ 0 1 1 2   1 4 1 2   r d r

=   - 2 π * 1 2   1 4 1 2 ∫ 0 1   r d r

= - π 2 2 r 2 2 r =   0 1

=   - π 4 2  

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ S x   d S     =   - π 4 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície. ∬ x y z d S , S é o cone com equações paramétricas x = u cos ⁡v , y = u s e n v , z = u , 0 ≤ u ≤ 1,0 ≤ v ≤ π 2 .
Calcule a integral de superfície. ∬ y d S S é o helicoide com o vetor paramétrico r u , v = u cos ⁡ v ,u sen ⁡ v ,v ,0 ≤ u ≤ 1 ,0 ≤ v ≤ π .
Calcule a integral de superfície. ∬ x + y + z d S S é o paralelogramo com as equações paramétricas x = u + v ,y = u - v ,z = 1 + 2 u + v ,0 ≤ u ≤ 2 ,0 ≤ v ≤ 1 .
Calcule a integral de superfície. ∬ x 2 + y 2 d S S é a superfície com o vetor paramétrico r u , v = 2 u v ,u 2 - v 2 , u 2 + v 2 ,u 2 + v 2 ≤ 1 .
Uma superfície S é formada pelo cilindro x 2 + y 2 = 1 ,- 1 ≤ z ≤ 1 , e por círculos no fundo e no topo. Suponha que você saiba que f é uma função contínua com f ± 1,0 , 0 = 2 , f 0 , ± 1,0 = 3 e f 0,