Calcular , onde T é a região delimitada por e z
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar:
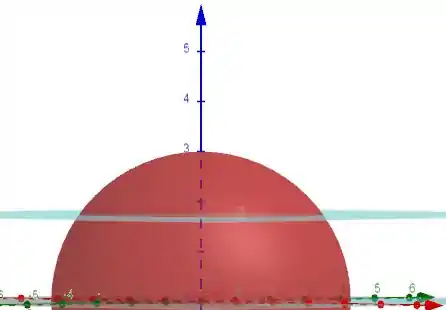
Então, o que faremos?
Vamos calcular o volume da semiesfera de 0 até o topo e subtrair do volume da semiesfera que vai de até o topo
Em coordenadas esféricas:
O raio é delimitado pelos valores de z. Quando
E o raio irá de
Quando
E neste caso o raio irá de:
O é o ângulo que o ponto pode fazer com o eixo x, na esfera esse ângulo vai de 0 até 360°:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo a primeira integral:
Sendo assim:
Vamos começar resolvendo:
Simplificando:
Resolvendo a segunda integral, sem levar em consideração agora o intervalo:
Vamos chamar:
De volta ao r:
Com o resultado podemos aplicar os intervalos:
Colocando nas integrais:
Aplicando o intervalo:
De boas ?