Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 12.4 - Ex. 2
Calcule a área do conjunto de todos os tais que .
Passo 1
Olá, galerinha! Vamos lá, vamos analisar a expressão, temos aqui que é uma elipse, e que a equação da elipse pode ser escrita da seguinte maneira:
E a gente consegue calcular a área dela pela seguinte fórmula:
Mas estamos em um capítulo de integral! Então vamos usar a integral para resolver essa questão!
temos que a expressão é uma elipse, e podemos ver ela na figura abaixo:
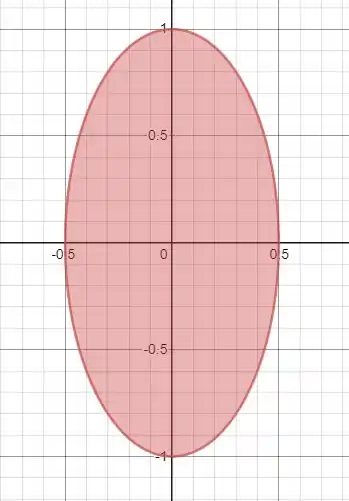
Vamos usar a expressão com igualdade para calcular a integral, e vamos calcular apenas a área do primeiro quadrante, e multiplicar o resultado por , assim obtemos a área total.
Vamos montar a integral, o limite de integral é de a e vamos integrar em função de , assim temos que isolar o na expressão:
Pronto, agora é só colocar na integral:
Passo 2
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Aqui vamos usar a substituição trigonométrica e para isso vamos usar o seguinte triângulo retângulo,
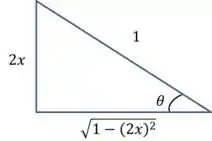
Note que,
Vamos usar a seguinte substituição:
Derivando:
Fazendo a substituição ficamos com:
Simplificando,
Agora vamos usar a seguinte identidade :
Vamos ter que usar outra identidade:
Aplicando-a:
Pronto, chegamos a duas integrais que dá pra calcular, vamos calcular as duas separadamente.
Passo 3
Com a primeira para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 4
Vamos para segunda,
Aqui vamis usar a Regra da Substituição
Vamos agora achar diferencial de , derivando:
Fazendo a substituição ficamos com:
Aqui, para achar as primitivas da função, vamos usar essa expressão da Tabela de Integrais Indefinidas:
Aplicando:
Passo 5
Agora é só juntar tudo:
Calma, não terminou ainda, não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo.
Então temos,
Substituindo,
Passo 6
Pronto, já encontramos a integral indefinida, perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com:
Aplicando,