Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 34
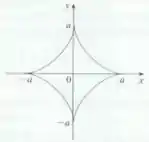
Calcule a área da região limitada pelo astroide (Os astroides foram explorados no Projeto de Laboratório na página 597).
Passo 1
Fala ai pessoal! Bora calcular uma área?
O que podemos tirar dessa questão? O asteroide é uma curva simétrica em relação aos eixos e , o que significa que a área em cada um dos quatro quadrantes do plano cartesiano é a mesma. Ou seja, podemos calcular a área de um quadrante e depois multiplicar por . Sacou?
Como vamos fazer isso?
- Encontrar os limites de integração;
- Encontrar a derivada da curva em relação a ;
- Substituir os na equação da área ;
- E por fim resolver a integral.
Vamos começar!
Passo 2
A primeira coisa que temos que colocar em mente quando fizermos exercícios de área é o intervalo que queremos. Então como estamos trabalhando com equações paramétricas a nossa variável independente de dentro da função é a que precisamos para definir o intervalo.
Nesse caso o astroide vai de até então substituiremos esses valores de x, isolando
Se
Se
Passo 3
Agora que já encontramos os intervalos podemos nos focar em resolver a integral. Mas antes disso vamos definir os valores que usaremos em função de
Sabendo que a área é definida por , precisamos definir
Passo 4
Tendo tudo definido podemos nos divertir com a integral:
Tirando o que for constante pra fora pra não nos confundirmos:
Para continuar nossa resolução precisamos lembrar de duas relações:
Passo 5
Substituindo então na integral:
Lembrando que :
Substituindo novamente pela relação sempre lembrando que o ângulo dobra:
Ajeitando a integral:
Passo 6
Bom, nos deparamos com outro probleminha que precisaremos novamente de uma relação. Nem sempre elas vão estar na ponta da língua, então quanto mais usarmos em exercícios desse tipo melhor.
Agora que temos tudo simplificado podemos resolver as integrais, lembrando que o numero de dentro do argumento passa multiplicando no denominador: