Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 24
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.
Passo 1
Opa, tudo tranquilo? Questãozinha de integral em coordenadas polares aqui, vamos lá!
Idealmente vamos plotar nossas curvas para termos ideia da área que a gente tá calculando.
A segunda curva é simples, apenas um círculo de raio 1 centrada na origem. Já no caso da primeira curva podemos plotar o gráfico atribuindo valores a :
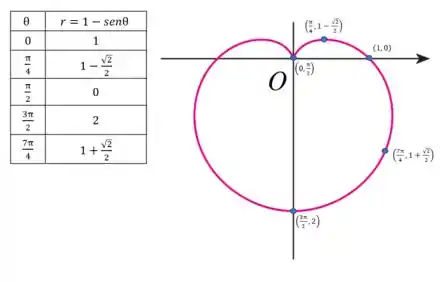
Dessa forma, temos que calcular a área da seguinte região sombreada:
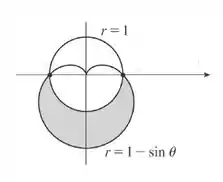
A área de uma curva em coordenadas polares é dada por
Então temos apenas que adaptar essa integral para o nosso caso e resolvê-la.
Passo 2
Para encontrar esse intervalo, no caso dessa questão, vamos precisar encontrar os pontos de interseção entre as duas curvas, já que queremos a área não da primeira curva nem da segunda curva, mas sim da região delimitada entre a primeira e a segunda.
Para isso, igualamos as duas curvas:
E
Assim, esses são os dois valores de no qual as curvas se intersectam.
Com essa informação e a figura para auxiliar, temos então o intervalo no qual nossa região de interesse está definida:
Pois a região sombreada está abaixo do eixo horizontal, ok? E não podemos esquecer que o ponto é coincidente com o ponto .
Então, o intervalo de integração seria
Passo 3
Continuando, falta a gente descobrir quem é o .
O é a própria parametrização. Mas como queremos descobrir a área entre a primeira e a segunda curva, vê se faz sentido pra vocês que a gente faça a área da curva de fora menos a área da curva de dentro?
Faz né?!
Assim, vamos ter dois , porque vamos ter duas áreas, ou seja, duas integrais, a da curva de fora e a da curva de dentro.
Então agora é só substituir e integrar esse negocio.
Passo 4
Vamos lá:
Trocando o por uma identidade trigonométrica:
Resolvendo a integral:
Reorganizando:
Aplicando os limites de integração:
Temos por fim que a área da região é: