Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.Revisão - Ex. 13

Calcule int 8 x^4 cos 2 x d x usando integração por partes tabulada.

Passo 1

Cara, esse é o tipo de integração que a gente usa quando uma das funções é um polinômio de grau mais alto. Aí a gente pode criar uma tabelinha que facilita as contas. Vem comigo!

A primeira coisa que a gente faz é derivar o polinômio até chegar em 0 , e preencher uma coluna inteira com os resultados.

Como nosso polininômio é 8 x^4 , fazemos assim:

(8 x^4)^' = 32 x^3

(32 x^3)^' = 96 x^2

(96 x^2)^' = 192 x

(192 x)^' = 192

(192)^' = 0

Chegamos em 0 , nossa tabelinha fica assim:

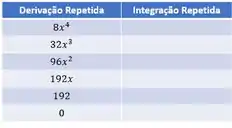
Passo 2

Agora a gente integra a outra função várias vezes para completar a tabela:

cos 2 x

Usando a substituição u = 2 x , em todas as integrais que forem feitas, a gente vê que ficam assim:

int cos 2 x d x = (s e n 2 x)/(2)

int (s e n 2 x)/(2) d x = - (cos 2 x)/(4)

int - (cos 2 x)/(4) d x = - (s e n 2 x)/(8)

int - (s e n 2 x)/(8) d x = (cos 2 x)/(16)

int (cos 2 x)/(16) d x = (s e n 2 x)/(32)

A tabelinha fica:

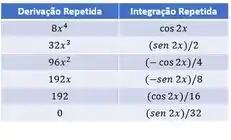
Tá linda!

Passo 3

A gente vai colocar umas setinhas inclinadas na tabela, alternando sinais, começando com + . E aí vamos fazer o produto entre as funções que estão ligadas pelas setinhas, multiplicando por - 1 se o sinal for de menos.

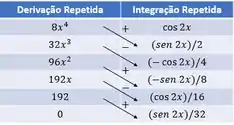
Depois a gente soma tudo e esse é o resultado da integral. Fica assim:

int 8 x^4 cos 2 x d x = 8 x^4 ((s e n 2 x))/(2) + 32 x^3 (cos 2 x)/(4) - 96 x^2 (s e n 2 x)/(8) - 192 x (cos 2 x)/(16) + 192 (s e n 2 x)/(32)

int 8 x^4 cos 2 x d x = 4 x^4 s e n 2 x + 8 x^3 cos 2 x - 12 x^2 s e n 2 x - 12 x cos 2 x + 6 s e n 2 x + C

Não podemos esquecer da constante de integração, porque isso não é uma integral definida.

Ufa! Conseguimos!

Resposta

int 8 x^4 cos 2 x d x = 4 x^4 s e n 2 x + 8 x^3 cos 2 x - 12 x^2 s e n 2 x - 12 x cos 2 x + 6 s e n 2 x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a equação que resulta se aplicarmos integração por partes à integral ∫ 1 x ln ⁡ x d x Com as escolhas: u = 1 ln ⁡ x E d v = 1 x d x Em qual sentido essa equação é válida? Em qual sentido é fals
Calcule a integral usando integração por partes tabulada. ∫ e a b s e n b x d x
Use as fórmulas de redução do Exercício 64 para calcular as integrais. ( a ) ∫ x 2 e 3 x d x ( b ) ∫ 0 1 x e - x d x
43-44 Calcule a integral fazendo uma substituição u e, depois, integrando por partes.44- ∫ cos ⁡ xd x
39-42 Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.40- Utilizando a estratégia do LIATE para calcular ∫ x 3 ln ⁡ xd x , deveríamos escolher u = x 3 e d v = ln ⁡ xd x .