Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.5 - Ex. 21
Calcule as dez primeiras somas parciais da série e faça o gráfico da sequência de termos e da sequência das somas parciais na mesma tela. Estime o erro ao usar a décima soma parcial para aproximar a soma total.
Passo 1
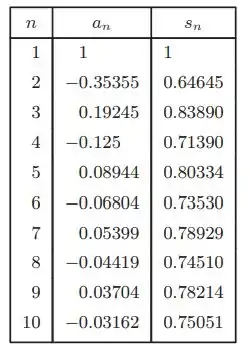
Galera, calculamos as primeiras dez somas parciais e colocamos na tabela a seguir:
Passo 2
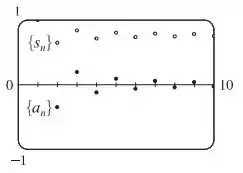
Show! Agora vamos fazer um gráfico da sequência de termos e da sequência das somas parciais na mesma tela:
Passo 3
Por último, vamos estimar o erro ao usar a décima soma parcial para aproximar a soma total, usando o Teorema da Estimativa de Séries Alternadas:
Resposta
Exercícios de Livros Relacionados
Use as seguintes etapas para mostrar que ∑ n = 1 ∞ - 1 n - 1 n = ln 2 Sejam h n e s n as somas parciais das séries harmônica e harmônica alternada.(a) Mostre que s 2 n = h 2 n - h n .(b) Do Exercíci
Mostre q a soma dos primeiros 2n termos da série 1 - 1 2 + 1 2 - 1 3 + 1 3 - 1 4 + 1 4 - 1 5 + 1 5 - 1 6 + … É a mesma dos primeiros n termos da série 1 1 * 2 + 1 2 * 3 + 1 3 * 4 + 1 4 * 5 + 1 5 * 6 +
Prove a afirmação do Teorema 15 de que sempre que uma série alternada que satisfaça as condições do Teorema 14 for aproximada por uma das suas somas parciais, então o resto (soma dos termos não utiliz
O limite L de uma série alternada que satisfaz as condições do Teorema 14 está entre os valores de quaisquer duas somas parciais consecutivas. Isso sugere o uso da média s n + s n + 1 2 = s n + 1 2 -
O que é uma série alternada? Qual teorema está disponível para determinar a convergência de tal série?