Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.4 - Ex. 15

Calcule a integral indefinida:

int (d x)/(sqrt(4 x + x^2))

Passo 1

Pessoal, essa integral é resolvida por substituição trigonométrica, mas, antes, devemos completar o quadrado dentro da raiz, vejamos como.

4 x + x^2 = underset((x + 2)^2)(ubrace x^2 + 4 x + 4) - 4 = (x + 2)^2 - 4

Com isso, a integral fica:

int (d x)/(sqrt((x + 2)^2 - 4))

Agora podemos usar a substituição trigonométrica.

Passo 2

Devemos saber qual substituição trigonométrica usar, como nós temos (x + 2)^2 - 2^2 no denominador, isso indica a substituição com a secante, como vocês podem ver a seguir no quadro de substituições com os respectivos triângulos e intervalos.

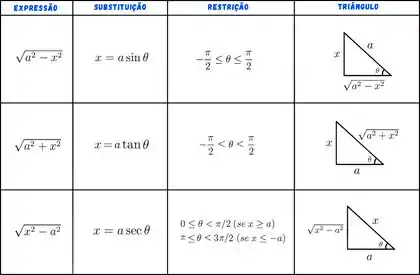
Olhando o quadrinho, percebemos que a substituição deve ser x + 2 = 2 sec theta . Façamos então a substituição:

[[x,+,2,=,2,sec theta],[d,x,=,2,sec theta,tan theta,d,theta]]

Dessa forma, (x + 2)^2 = 4 sec^2 theta -> (x + 2)^2 - 4 = 4 sec^2 theta - 4 = 4 overset(tan^2 theta)(obrace (sec^2 theta - 1)) = 4 tan^2 theta .

Passo 3

Agora vamos manipular a expressão da integral e trocar a variável:

int (d x)/(sqrt((x + 2)^2 - 4)) = int (2 sec theta tan theta d theta)/(sqrt(4 tan^2 theta)) = (2)/(2) int (sec theta tan theta d theta)/(tan theta)

= int sec theta d theta = ln | sec theta + tan theta | + C

Aqui usamos int s e c theta d theta = ln | sec theta + tan theta | + C .

Passo 4

Como a integral indefinida foi dada na variável x , devemos dar a resposta nesta variável. Sendo x + 2 = 2 sec theta -> sec theta = (x + 2)/(2) , temos:

int (d x)/(sqrt((x + 2)^2 - 4)) = = ln | sec theta + tan theta | + C

Para achar tan theta nós olhamos o triângulo da substituição com s e c construído no inicio e utilizamos essas relações trigonométricas. Temos então:

tan theta = (sqrt(x^2 - a^2))/(a) -> tan theta = (sqrt(( x + 2 )^2 - 4))/(2)

No triângulo está x , mas nós efetuamos a substituição usando x + 2 , então basta trocar.

Dessa forma, o resultado da integral será:

int (d x)/(sqrt((x + 2)^2 - 4)) = ln |(x + 2)/(2) + (sqrt(( x + 2 )^2 - 4))/(2)| + C = ln |(x + 2)/(2) + (sqrt(4 x + x^2))/(2)| + C

= ln |(x + 2 + sqrt(4 x + x^2))/(2)| + C

Resposta

int (d x)/(sqrt(4 x + x^2)) = ln |(x + 2 + sqrt(4 x + x^2))/(2)| + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

37-48. Calcule a integral.37. ∫ d x x 2 - 4 x + 5
37-48. Calcule a integral.39. ∫ d x 3 + 2 x - x 2
1-26. Calcule a integral.21. ∫ 0 1 5 x 3 1 - x 2 d x
A integral: ∫ x x 2 + 4 d x Pode ser calculada ou por substituição trigonométrica ou pela substituição u = x 2 + 4 . Calcule-a das duas maneiras e mostre que os resultados são equivalentes.
37-48. Calcule a integral.40. ∫ d x 16 x 2 + 16 x + 5