Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.5 - Ex. 11
Calcule a integral indefinida.
Passo 1
Eaee, belezinha?? Bom... queremos calcular a seguinte integral indefinida:
Bem... aqui vamos usar a Regra da Substituição, então mãos a massa!!
Para isso temos que chamar algo de , repare que temos uma multiplicação de duas funções, qual será a nossa ?
A mais complicada! Então chamaremos tudo que está dentro dos parênteses de , em seguida derivamos em função de , para encontrar . Lembre-se que queremos facilitar, então a intenção é que todo nosso resto da função seja o , às vezes precisamos dar uma manipuladinha, vamos ter algo assim:
Onde é uma constante que vamos descobrir quando derivarmos .
Para revolver essa integral, vamos usar a tabela de primitivas:
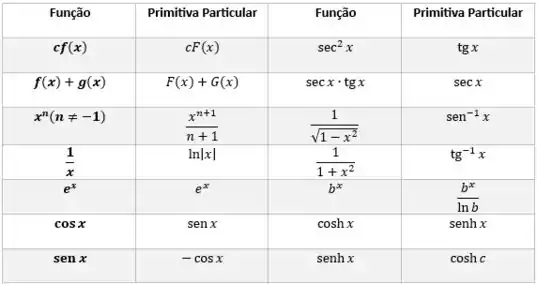
Depois de resolvida, temos que voltar para seu valor original!
Agora bora aplicar!! 😉
Passo 2
Vamos fazer uma mudança de variável, chamando tudo que está dentro dos parênteses de :
Vamos agora achar a derivada de ,
Derivando e isolando o .
Comparando com a nossa integral original:
Percebe que temos algo muito próximo do que está dentro dos colchetes? Então podemos dar uma arrumadinha para ficar idêntico, note que só precisamos passar o dividindo:
Agora vamos reescrever nossa integral:
Agora fica simples de resolver, vamos lá.
Passo 3
Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais do passo 1:
Reescrevendo nossa integral para facilitar:
Colocar o para fora da integral:
Aplicando a primitiva da potência:
Passo 4
Calma, não terminou ainda, não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo, no caso aqui foi
Primeiro substituímos:
Encontramos a primitiva:
E agora voltamos para o valor de :
Prontinho, já temos a nossa resposta!
Entendeu? Responde Aí!
