Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.2 - Ex. 51
Calcule a integral indefinida. Ilustre e verifique se sua resposta é razoável colocando em um gráfico um integrando e sua primitiva (tome ).
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular a integral indefinida da função e esboçar o gráfico dessa função junto com a sua antiderivada, usando .
A antiderivada será o resultado da nossa integral, que vamos chamar de . Além disso, é uma constante de integração, que aparece porque se trata de uma integral indefinida, beleza?
Agora pra resolver essa integral, vamos usar a técnica de substituição, chamando:
Dessa forma, temos:
Substituindo isso na nossa integral, fica mais fácil obter a nossa antiderivada.
Vamos lá!
Passo 2
Substituindo e , vamos ter:
Agora, a gente precisa lembrar da seguinte propriedade trigonométrica:
Então, usando essa propriedade na integral, ficamos com:
Colocando a constante do lado de fora da integral:
Integrando, temos:
Onde é a nossa constante de integração. Aplicando a distributiva no produto:
Agora vamos voltar pra nossa variável original, usando . Assim, temos:
E como :
Passo 3
Agora só falta a gente esboçar o gráfico de e da sua antiderivada . Assim, temos e , olha só:
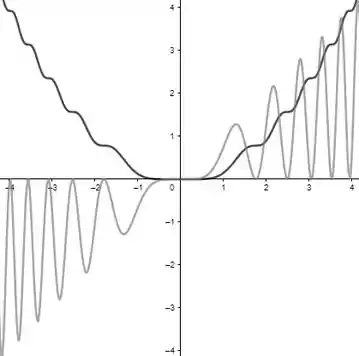
Vemos no gráfico que isso é razoável, pois aumenta onde é positivo e diminui onde é negativo.
Note também que é uma função ímpar e é uma função par.
Prontinho, galera! Até a próxima! 😉