Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 40
Calcule a integral, interpretando-a em termos das áreas.
Passo 1
Bom queridões... nessa questão temos a seguinte integral:
E devemos calcula-la, interpretando-a em termos de áreas.
Sabemos que a integral nada mais é do que a área abaixo de uma função.
E sabemos como é o gráfico da função , ele é aquele gráfico em V, fica mais ou menos assim, ó:
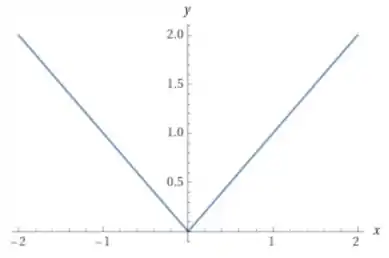
Como queremos a função , o que temos na verdade é esse gráfico de cima transladado em unidades para a direita, logo, temos o seguinte:
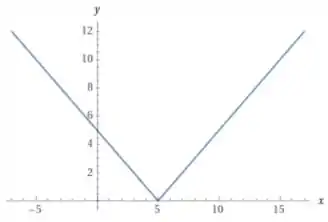
Aqui vamos precisar calcular a área entre até que nada mais é do que a integral pedida. Bora lá?
Passo 2
Vamos lá, a integral pode ser interpretada como a área sob o gráfico de entre e , que são os limites de integração do gráfico.
Vamos então ter a figura abaixo:
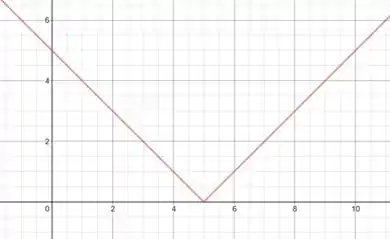
Pela figura vemos que é a área de dois triângulos, um com base e altura e o outro com base e altura , assim a integral é a soma dessas áreas: