Ligue a equação diferencial a seu campo de direções (I – IV). Dê as razões para sua resposta.

6.

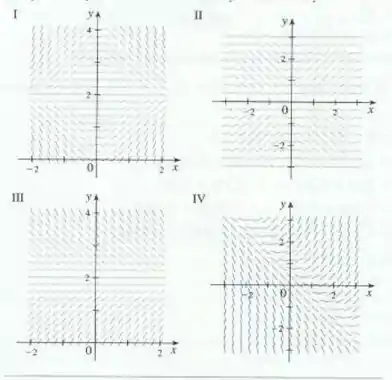
Precisamos encontrar qual dos campos de direção apresentados corresponde a equação

Podemos começar analisando o que acontece quando , isso ocorre quando é um inteiro múltiplo de (como ). Então em temos uma reta horizontal e em também. O único campo que satisfaz essas duas condições é o II.