Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.4 - Ex. 4

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

Passo 1

Fala, galera! Tudo blzinha?

Então, nessa questão precisamos calcular essa integral de linha abaixo por dois métodos:

(a) diretamente; ou

(b) utilizando o Teorema de Green

∫ C x 2 y 2   d x + x y   d y

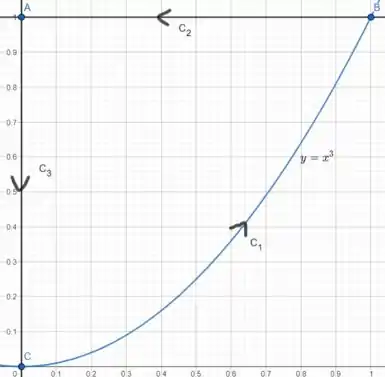
O enunciado nos dá informações sobre a região C , que é definido pelo arco de parábola y = x 2 de 0,0   a   ( 1,1 ) e pelos segmentos de reta 1,1   a   ( 0,1 ) e de 0,1   a   0,0 . Show?

Para resolvermos esse exercício, no item (a) vamos dividir as curvas C em 3   partes e parametrizar cada uma delas.

Para a segunda parte do exercício (item (b)), iremos utilizar uma fórmula para o teorema de Green e calcular.

Passo 2

Para o item (a), vamos dividir a curva C em 3 (por conta dos pontos), ficando com C 1 ,   C 2   e   C 3 . Temos que uma propriedade das integrais de linha é

∫ C F → ⋅ d r → = ∫ C 1 F → ⋅ d r → + ∫ C 2 F → ⋅ d r → + ∫ C 3 F → ⋅ d r →

Assim, precisamos apenas parametrizar as curvas e calcular as integrais separadamente.

Temos que a primeira curva, C 1 , podemos chamar x = t e y = t 2 , com um intervalo 0 ≤ t ≤ 1 . Precisamos de d x e d y também. Derivando, chegamos que d x = d t e d y = 2 ⋅ t

C 2 podemos será a reta que vai de 1,1   a   ( 0,1 ) . Temos que y é constante em 1 e apenas x varia. Podemos fazer então que y = 1 e x , por se tratar de uma reta que vai de 1 até 0, será x = 1 - t , onde 0 ≤ t ≤ 1 e com d x = - d t e d y = 0

Para C 3 será algo parecido a C 2 por se tratar também de uma reta com uma das componentes constantes. Assim, temos que x = 0 e y = 1 - t , onde 0 ≤ t ≤ 1 e com d x = 0 e d y = - d t

Substituindo na integral agora, temos que

∫ C x 2 y 2   d x + x y   d y

∫ C 1 x 2 y 2   d x + x y   d y + ∫ C 2 x 2 y 2   d x + x y   d y + ∫ C 3 x 2 y 2   d x + x y   d y

Calculando em C 1 primeiro, temos que

∫ 0 1 t 6   d t + t 3 2 t   d t

t 7 7 + 2 ⋅ t 5 5 0 1 = 1 7 + 2 5

C 2 será:

∫ 0 1 1 - t 2 ⋅ 1 ⋅ - d t + 1 - t ⋅ 0

- t + t 3 3 - 2 t 2 2 0 1

- 1 - 1 3 + 1 = - 1 3

Para C 3

∫ 0 1 0   d t + 0   d t = 0

Somando então, temos que nossa integral resulta em

1 7 + 2 5 - 1 3 = 22 105

Passo 3

Usando agora o teorema de Green (item (b)), temos que

∫ C F → ⋅ d r → = ∫ ∫ D ∂ Q ∂ x - ∂ P ∂ y d A

Calculando então a integral dupla, temos que

∫ ∫ D ∂ ∂ x x y - ∂ ∂ y x 2 y 2 d A

∫ 0 1 ∫ x 2 1 y - 2 x 2 y d x d y

Resolvendo de dentro para fora, teremos:

∫ 0 1 y 2 2 - x 2 y 2 x 2 1 d x

∫ 0 1 1 2 - x 4 2 - x 2 + x 6 d x

1 2 ⋅ x - x 5 10 - x 3 3 + x 7 7 0 1

Substituindo pelos limites de integração, chegaremos a:

1 2 - 1 10 - 1 3 + 1 7 = 22 105

Resposta

∫ C x 2 y 2   d x + x y   d y = 22 105

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a fórmula da área do teorema de Green fornecida acima para encontrar as áreas das regiões delimitadas pelas curvas nos Exercícios 25-28A astroide r(t) = (cos3 t)i + (sen3 t)j, 0 ≤ t ≤ 2p
Aplique o teorema de Green para calcular as integrais nos Exercí-cios 21-24 ∮ C 2 x + y 2 d x + ( 2 x y + 3 y ) d y C: Qualquer curva fechada simples no plano para o qual o teorema de Green é válido.
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C. F = x 1 + y 2 i + tg - 1 ⁡ y j
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C.F = (x2 + 4y)i + (x + y2)jC: O quadrado limitado por x
Nos Exercícios 5-14, utilize o teorema de Green para encontrar a circulação em sentido anti-horário e o fluxo exterior para o campo F e a curva C.F = (y2 – x2)i + (x2 + y2)jC: O triângulo limitado por