Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 15
Verifique o Teorema de Green usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla.
consiste de um segmento de reta de para seguido do arco de curva de para
Passo 1
E aí, galera! Tranquilo?
Nossa questão pede para verificarmos o Teorema de Green, que traz a equação:
Onde
consiste de um segmento de reta de para seguido do arco de curva de para
Para resolver essa questão temos que usar um sistema de computação algébrica para calcular tanto a integral de linha:
Quanto a integral dupla:
Para a integral de linha vamos ter que parametrizar nossa curva em duas curvas e e montar sua integral. Depois é só pedir para o SCA calcular o valor da integral.
Para a integral dupla, calculamos as derivadas parciais, substituímos na equação e achamos os limites de integração a região limitada pela curva . Daí montamos a integral e pegamos o resultado do SCA.
Vamos lá!
Passo 2
A curva e região são exibidas abaixo.
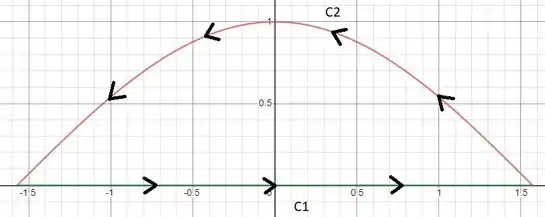
Primeiro, vamos calcular pela integral de linha. Para facilitar a nossa vida, vamos quebrar em dois trechos: .
Para o trecho , precisamos antes de tudo parametrizá-la. Aqui temos um variando e constante (e igual a zero). Assim,
Assim,
Substituindo , e , :
Somando esses termos, temos zero!
Passo 3
Agora, vamos olhar para a segunda curva . Parametrizando a curva é:
Assim,
Substituindo , e , :
Rearranjando os termos:
Fazendo uso de um sistema de computação algébrica, chegamos ao seguinte resultado:
Por fim, para achar a integral da curva total, somamos a integral da curva e :
Então:
Passo 4
Agora, vamos olhar para a integral dupla!
Precisamos calcular essas derivadas parciais aí de cima. Isso é moleza!
Desse modo, podemos escrever nossa integral dupla como:
Fazendo uso de um sistema de computação algébrica, chegamos ao seguinte resultado:
Depois de muita conta, verificamos o Teorema de Green, já que a integral de linha e a integral dupla são iguais!