Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 7

Verifique que

∫ γ P d x + Q d y = ∬ B ∂ Q ∂ x - ∂ P ∂ y d x d y

Onde B é o triângulo de vértices 0,0 , 1,0 e 1,1 ; γ é a fronteira de B orientada no sentido anti-horário, P x , y = x 2 - y e Q x , y = x 2 + y .

Passo 1

A curva em questão é dada pela imagem a baixo que criamos no software Geogebra

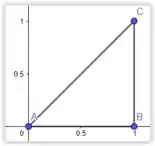
O Sentido que devemos adotar é o anti-horário, ou seja, A → B → C → A

Passo 2

Vamos fazer por partes, no caso, 3 partes. Assim

Para γ 1 A → B

γ 1 t = t , 0 ,   0 ≤ t ≤ 1

Com

d γ 1 t = ( d t , 0 )

Para γ 2   B → C

γ 2 t = 1 , t ,   0 ≤ t ≤ 1

Com

d γ 2 t = ( 0 , d t )

Para γ 3   C → A

γ 3 t = 1 - t , 1 - t ,   0 ≤ t ≤ 1

Com

d γ 3 t = ( - d t , - d t , 0 )

Passo 3

Assim teremos que

∫ γ x 2 - y d x + x 2 + y d y

Que substituindo nossas parametrizaçãos, teremos

= ∫ 0 1 t 2 d t + 1 + t d t + ( 1 - t 2 - ( 1 - t ) ) ( - d t ) + ( 1 - t 2 + 1 - t ) - d t

Que nos dá

∫ 0 1 - t 2 + 5 t - 1 d t = - t 3 3 + 5 2 t 2 - t 0 1 = - 1 3 + 5 2 - 1 = - 2 + 15 - 6 6 = 7 6

Passo 4

Agora vamos verificar a condições solicitada no enunciado, calculando

∬ B ∂ Q ∂ x - ∂ P ∂ y d x d y

Primeiro vamos definir nosso B .

Por se tratar de um triângulo, podemos fazer B = x , y ∈ R 2 0 ≤ x ≤ 1   e   0 ≤ y ≤ x }

Outro ponto importante fazer

∂ Q ∂ x - ∂ P ∂ y = ∂ x 2 + y ∂ x - ∂ x 2 - y ∂ y = 2 x + 1

Assim teremos

∫ 0 1 ∫ 0 x 2 x + 1 d y d x

Que podemos simplesmente resolver fazendo

∫ 0 1 2 x + 1 y 0 x d x = ∫ 0 1 2 x 2 + x d x

E finalmente

2 x 3 3 + x 2 2 0 1 = 2 3 + 1 2 = 4 + 3 6 = 7 6

Resposta

7 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C y d x - x d y C é o círculo com centro na origem e raio 1.
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C y d x - x d y C é o círculo com centro na origem e raio 1.
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C x y 2 d x + x 3 d y C é o retângulo com vértices 0,0 , 2,0 , 2,3 e 0,3 .
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C x y 2 d x + x 3 d y C é o retângulo com vértices 0,0 , 2,0 , 2,3 e 0,3 .
15. Dado o campo vetorial f → = y x 2 + y 2 , x x 2 + y 2 , mostrar que ∮ C f → ⋅ d r → = 0 para toda curva fechada simples C, suave por partes, que circunda a origem.