Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 10
Sejam duas funções de classe tais que, para todo em , . Seja o conjunto de todos tais que , . Seja a fronteira de orientada no sentido antí-horário. Prove que
Onde é suposta de classe num aberto que contém .
Passo 1
Pelo enunciado, consideremos funções de classe tais que , . E ainda seja nosso
Ou seja,
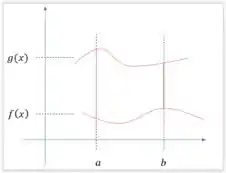
Assim faremos o seguinte
Passo 2
Assim teremos
Agora se fomos pela integral de linha. Para as integrais relacionadas as retas paralelas ao eixo , temos que nosso , logo as integrais são nulas. Com isso ficamos apenas com as parametrizações que levam nossas funções. Assim teremos
Fazendo temos
E desta forma temos que
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y 2 d x + x 2 y d y C é o retângulo com os vértices em 0,0 , 5,0 , 5,4e( 0,4 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x y d x + x 2 y 3 d y C é um triângulo com os vértices em 0,0 , 1,0e( 1,2 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y 2 d x + x 2 y d y C é o retângulo com os vértices em 0,0 , 5,0 , 5,4e( 0,4 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y d x - x d y C é uma circunferência com centro na origem e r a i o = 4 .