Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.4 - Ex. 1a

Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green.

C é o retângulo com vértices , , e .

Passo 1

Olá, tudo bem?

Vamos ver o que a questão quer.

Nessa letra a), ele quer que calculemos a integral de linha

Diretamente, usando a definição, onde é a linha de um retângulo representado pelos vértices dele.

Na letra b), teremos que utilizar o Teorema de Green

Que diz que podemos transformar uma integral de linha em uma integral dupla utilizando a relação acima.

Onde, na integral de linha é tudo que está ao lado de , é tudo que está ao lado de e é o contorno da curva. Nessa questão são os lados do retângulo!

E na integral dupla que vamos fazer, é o interior da curva que precisa estar orientada positivamente. Que é a área do retângulo nesse caso!

É a derivada parcial de em relação à ,

É a derivada parcial de em relação à e

E por que faríamos isso?

Bem, essa integral de linha não é muito complicada de resolver, mas existem outras que são quase impossíveis de resolver pela definição. Nesses casos, o teorema facilita nossa vida.

Portanto, como essa resolução é da letra a)

Vamos resolver a integral de linha dividindo a região em que representa os lados desse retângulo e depois calcular tudo.

Show?

Passo 2

Primeiro, vamos dividir nosso retângulo em curvas:

Vamos fazer um desenho para facilitar a compreensão

Agora, cada reta dessa será uma curva, que serão .

Assim:

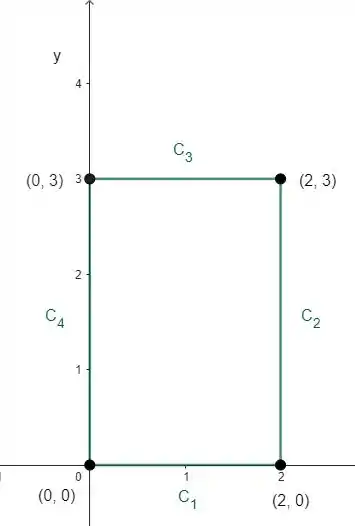
Então, a região da nossa integral de linha é dada pela união das 4 curvas:

Note que orientei a curva no sentido anti-horário, que sai da origem, vai para a direita onde , depois sobe para , vai para esquerda onde e volta para a origem.

Nas coordenadas uma curva orientada positivamente é uma curva orientado no sentido anti-horário.

Porém um jeito mais fácil de orientar a curva é pensar que você está andando nas bordas delas, e se o interior dela estiver à sua esquerda, ela está orientada positivamente!

Portanto,