Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.2 - Ex. 7
Calcule a integral de linha, onde é a curva dada.
consiste nos segmentos de reta de a e de a .
Passo 1
Faala, galera!
Nessa questão temos que calcular uma integral de linha sobre uma curva que ela descreveu.
consiste nos segmentos de reta de a e de a .
Percebe que como o diferencial dentro da integral de linha é e , nós estamos no caso vetorial! Ou seja, é a integral sobre um campo vetorial, que podemos escrever assim:
Onde
Bom, nesse caso, pra calcularmos a integral, temos que fazer:
Onde , com é uma parametrização da curva .
Mas como a nossa curva é dividida em dois segmentos, vamos tratar eles separados:
Então nosso primeiro passo vai ser desenhar essas curvas, pra conseguirmos parametrizar, depois vamos calcular as , e então aplicarmos a fórmula da integral de linha pra cada uma delas!
Passo 2
As curvas e são dois segmentos de reta, que ligam os pontos a , e a . Então, desenhando isso temos:
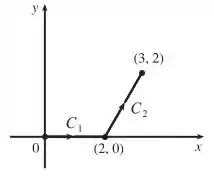
Vamos parametrizar cada pedaço da curva separadamente.
No segmento de reta , nós vemos que o varia, mas o permanece igual a zero. Então vamos definir o como o próprio parâmetro e constante igual a :
Como vai de até :
Já a reta , observamos que tanto quanto variam. Então vamos colocar em função de , por ser uma reta, essa função é da seguinte forma:
Quando:
Substituindo esses valores na nossa equação, vamos obter o seguinte sistema:
Subtraindo a primeira equação da segunda, temos que:
Pela segunda equação, podemos substituir o valor de e encontrar o valor de :
Logo:
Vamos definir como nosso parâmetro e por essa expressão:
Como vai de até :
Passo 3
Agora, calculamos as derivadas das parametrizações:
Para :
Para achar , derivamos as duas componentes em função de :
E para :
Para achar :
Passo 4
Finalmente, vamos aplicar as integrais de linha.
Lembrando que
Primeiro, para , temos:
Então:
Calculando:
Pra fazer esse produto escalar, multiplicamos cada uma das coordenadas correspondentes:
Então:
Passo 5
Agora para :
Então:
Fazendo as contas:
Multiplicando coordenada a coordenada:
Resolvendo a integral:
Calculando:
Então a integral fica:
Passo 6
A nossa integral é a soma dessas duas que calculamos, então:
Então: