Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 29

(a) Calcule a integral de linha ∫ C F → ∙ d r → , onde

F → x ,   y = e x - 1   i ^ + x y   j ^ e C é dada por r → t = t 2   i ^ + t 3   j ^ ,     0 ≤ t ≤ 1

(b) Ilustre a parte (a) utilizando uma calculadora gráfica ou um computador para desenhar C e os vetores do campo vetorial correspondentes a t = 0 ,     1 2 e 1 (como na Figura 13 ).

Passo 1

Falaa, pessoal!

Nessa questão precisamos calcular uma integral de linha de um campo vetorial F → sobre uma curva C .

Vamos lembrar que pra calcular uma integral de linha sobre uma curva parametrizada por r → t ,   a ≤ t ≤ b , fazemos:

∫ C F → ∙ d r → = ∫ a b F → r → t ∙ r ' → t   d t

Então na letra (a), vamos fazer isso!

Já na letra (b), vamos usar uma calculadora gráfica (no caso, vai ser o GeoGebra) pra desenhar a curva e os vetores de F → em três pontos.

Primeiro, vamos calcular quem são esses pontos e vetores, e depois jogar tudo no GeoGebra.

Passo 2

(a)

Pra calcular a integral de linha, começamos calculando o F → r → t

F → = e x - 1 , x y

r → = t 2 , t 3

Então, vamos substituir x por t 2 e y por t 3 na expressão de F → :

F → r → t = e t 2 - 1 , t 5

Agora, pra calcular r ' → t , vamos derivar cada uma das coordenadas de r → em função de t :

r ' → t = 2 t , 3 t 2

Então,

∫ C F → ∙ d r → = ∫ 0 1 F → r → t ∙ r ' → t   d t =

= ∫ 0 1 e t 2 - 1 ,   t 5   .   2 t ,   3 t 2   d t

Fazemos o produto escalar multiplicando coordenada a coordenada de um vetor com a correspondente no outro e somando. Ou seja:

= ∫ 0 1 e t 2 - 1 ∙ 2 t + t 5 ∙ 3 t 2   d t =

= ∫ 0 1 2 t e t 2 - 1 + 3 t 7   d t

Passo 3

Agora é só resolver a integral obtida:

∫ 0 1 2 t e t 2 - 1 + 3 t 7   d t =

Separamos em duas integrais:

= ∫ 0 1 2 t e t 2 - 1   d t + ∫ 0 1 3 t 7   d t =

Pra primeira integral, vamos fazer uma substituição u = t 2 - 1 :

d u = 2 t d t

u 0 = - 1

u 1 = 0

Então:

= ∫ - 1 0 e u   d u + ∫ 0 1 3 t 7   d t =

E agora podemos calcular as integrais:

= e u - 1 0 + 3 t 8 8 0 1 =

= e 0 - e - 1 + 3 ∙ 1 8 - 0

Calculando:

= 1 - 1 e + 3 8

⇒   ∫ C F → ∙ d r → = 11 8 - 1 e

Passo 4

(b)

Vamos calcular o valor de F → para t = 0 , 1 2 , 1 .

Para cada valor de t , primeiro vamos caluclar r → t , depois vamos substituir esse resultado na expressão de F → .

Para t = 0 :

r → 0 = 0,0

F → = e - 1 , 0

Para t = 1 2 :

r → 1 2 = 1 2 2 , 1 2 3

= 1 2 , 1 2 2

Então:

F → = e 1 2 - 1 , 1 2 ∙ 1 2 2

= e - 1 2 , 1 4 2

Para t = 1 :

r → 1 = 1,1

F → = e 1 - 1 , 1 ∙ 1

= 1,1

Passo 5

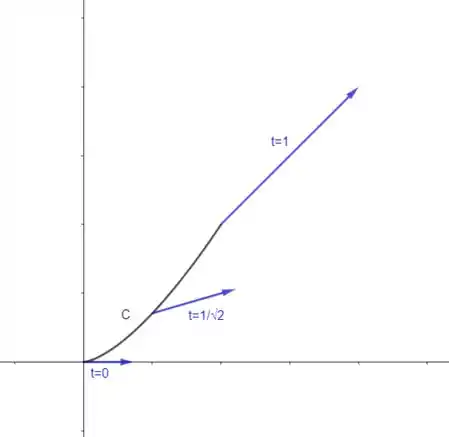
Pra plotar isso no GeoGebra, usamos esses comandos:

Pros vetores, precisamos inserir o ponto inicial, que é r → t e o ponto final, que é r → t + F → r → t para cada valor de t .

Resposta

(a)

∫ C F → ∙ d r → = 11 8 - 1 e

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura abaixo mostra o campo vetorial F → x , y = 2 x y , x 2 e três curvas que começam em ( 1,2 ) e terminam em ( 3,2 ) . Explique por que ∫ C F → ⋅ d r → tem o mesmo valor para as três curvas.Qual
A posição de um objeto com massa m no instante t é r → t = a t 2 i ^ + b t 3 j ^ , 0 ≤ t ≤ 1 .(a) Qual é a força que age sobre o objeto no instante t ?(b) Qual é o trabalho realizado pela força durant
Determine o trabalho realizado pelo campo de força F → x , y = x 2 i ^ + y e x j ^ em uma partícula que se move sobre a parábola x = y 2 + 1 de ( 1,0 ) a ( 2,1 ) .
Calcule o valor da integral de linha, onde C é a curva dada. ∫ C e x d x C é o arco da curva x = y 3 indo de ( - 1 , - 1 ) até ( 1,1 )