Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 30
(a) Calcule a integral de linha , onde
e é dada por
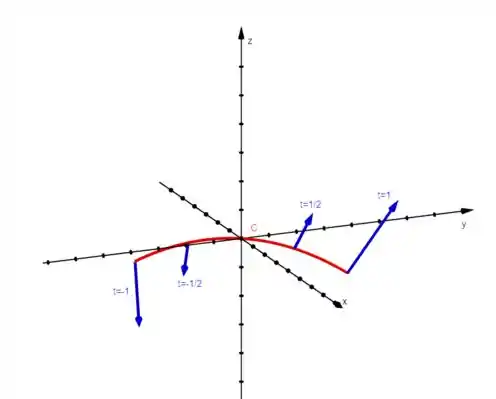
(b) Ilustre a parte (a) utilizando um computador para desenhar e os vetores do campo vetorial correspondentes a e (como na Figura ).
Passo 1
E aii, galera!
Essa questão ta pedindo duas coisas pra gente
Primeiro, precisamos calcular uma integral de linha de um campo vetorial sobre uma curva .
Depois, vamos desenhar essa curva e alguns vetores de usando um software (no nosso caso, vai ser o GeoGebra).
Pra calcular a integral de linha, vamos usar:
Onde é uma parametrização de .
Pro desenho, vamos calcular quais são os pontos e os vetores correspondentes a cada valor de e . Depois, jogamos tudo no GeoGebra!
Passo 2
(a)
Vamos calcular .
Então, vamos substituir na expressão de :
Já para , vamos derivar cada uma das componentes de em função de :
Então, a integral é:
Vamos multiplicar as coordenadas correspondentes e somar, para calcular o produto escalar:
Passo 3
Calculando a integral:
Então:
E achamos o valor da integral:
Passo 4
(b)
Agora vamos calcular os valores de para e .
Primeiro calculamos , depois aplicamos esse resultado em .
Para :
Para :
Para :
Para :
Passo 5
Os comandos que vamos usar no GeoGebra são:
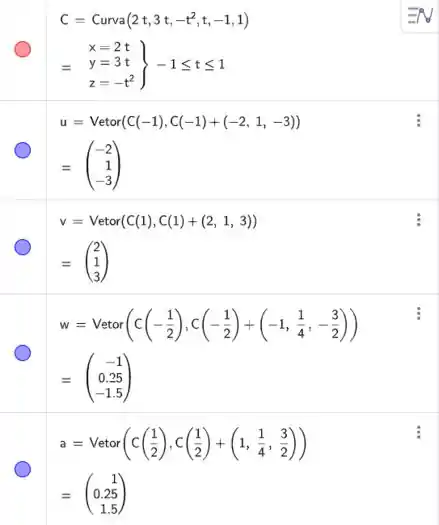
Pros vetores, precisamos inserir o ponto inicial, que é e o ponto final, que é para cada valor de .
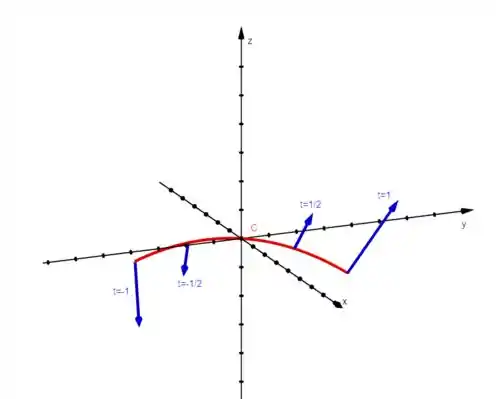
Resposta
(a)
(b)
