Exercícios de Caso Vetorial no R³ - Lista de Exercícios Resolvida

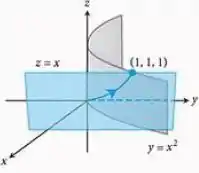
O campo é o campo de velocidades de um escoamento no espaço. Encontre o escoamento de até ao longo da curva de interseção do cilindro e do plano . (Sugestão: use como parâmetro.)

Calcule a integral de linha , onde é a fronteira da parte do plano no primeiro octante.

Calcule

Onde e é a interseção das superfícies e , percorrida no senti anti-horário quando vista da origem.

Seja a interseção do cilindro com o semiplano , , percorrida de modo que sua projeção no plano tenha sentido anti-horário e seja . Calcule a integral

Considere o campo de vetores e considere a curva parametrizada pela função vetorial com . Calculando a integral

Obtemos:

Calcule

Onde e é a interseção das superfícies e , percorrida no senti anti-horário quando vista da origem.

Calcule , nos seguintes casos:

(c) ; é o segmento de reta da origem ao ponto .

Calcule , nos seguintes casos:

(d) ; é o arco da parábola , e ; .

O movimento de uma partícula de massa unitária no intervalo de tempo é descrito pela curva parametrizada

c) Calcule o trabalho realizado pela força atuando sobre a partícula entre os instantes e .

Considere o campo de vetores e considere a curva C parametrizada pela seguinte função vetorial com . Calculando a integral temos:

1. 0

O campo de forças atua sobre uma partícula transladando-a ao longo da curva interseção das superfícies e , orientada de modo que sua projeção no plano seja percorrida uma vez, no sentido horário. Calcule o trabalho realizado por

Encontre o trabalho realizado pela força

No sentido de crescente sobre o caminho

1. Calcule , do ponto ao ponto , ao longo dos seguintes cainhos:

1. Segmento de reta

1. Calcule , do ponto ao ponto , ao longo dos seguintes cainhos:

1. interseção das superfícies e .

Calcule sendo a curva dada pela interseção das superfícies e , percorrida de a

Calcular em que é a hélice definida por , e o campo vetorial definido por .

(a)

(b)

(c)

(d)

(e)

Calcule

Sendo a curva de interseção das superfícies e percorrida de modo que sua projeção no plano seja percorrida no sentido anti-horário.

Calcule

Onde e é o segmento de reta que liga o ponto ao ponto .

1. Calcule o trabalho realizado pela força para deslocar uma partícula ao longo da curva interseção das superfícies e , orientada do ponto a .

Calcule a integral de linha, onde é a curva dada.

(Capítulo 16.3 – Exercício 15)

(a) Determine uma função tal que e (b)Use a parte (a) para calcular sobre a curva dada.

é o segmento de reta de

(Cap.16.3 - Exercício 18) (a) Determine uma função tal que e (b) use a parte (a) para calcular sobre a curva dada.

,

(Cap.16.2 - Exercício 42) A força exercida pela carga elétrica colocada na origem sobre uma partícula carregada em um ponto com vetor posição é , onde é uma constante (veja o Exemplo da seção ). Encontre o trabalho feito quando a partícula se move ao longo de uma linha reta de a .

Calcular a integral de linha onde e é o segmento de reta que liga o ponto ao ponto .

(3) O valor da integral do campo vetorial ao longo da curva parametrizada por , , é:

7. Calcule , sendo dados:

a) e , .

7. Calcule , sendo dados:

b) e , .

7. Calcule , sendo dados:

e) e , .

9. Uma partícula desloca-se em um campo de forças dado por . Ache o trabalho realizado por no deslocamento da partícula de até , sendo dados

a) , ; .

9. Uma partícula desloca-se em um campo de forças dado por . Ache o trabalho realizado por no deslocamento da partícula de até , sendo dados

b) , ; .

Seja a curva dada pela intersecção do paraboloide com o cilindro , orientade de modo que sua projeção no plano seja percorrida uma ver no sentido anti-horário. Calcule no seguinte caso:

Seja para .

Calcule , onde .

A curva dada por:

Representa o formato de um arame.

1. Encontre uma parametrização para
2. Escreva duas integrais definidas no parâmetro que expressem respectivamente:

- a carga do arame, se a densidade é dada por

- o trabalho que realiza o campo ao longo do arame

Calcule , onde

E é a curva obtida com interseção do cilindro com o plano .

Seja a curva parametrizada:

1. Calcule equações implícitas para .
2. Faça um esboço da imagem de .
3. Calcule as equações implícitas da reta tangente a em .
4. Calcule a integral de linha

Calcule , onde

e é a interseção de e , com e , percorrida do ponto ao ponto .

Seja a interseção do cilindro com o semiplano , , percorrida de modo que sua projeção no plano tenha sentido anti-horário e seja . Calcule a integral

Calcule , nos seguintes casos:

(a) ; é a fronteira da região , orientada no sentido horário.

Calcule , nos seguintes casos:

(e) ; consiste do segmento de reta de a , seguido do seguimento de reta de a .