Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.7 - Ex. 27

Calcule a integral de superfície ∫ ∫ S   F ⋅ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação positiva (para fora).

F x ,   y ,   z = y   j - z   k

S é formada pelo paraboloide y = x 2 + z 2   ,     0 ≤ y ≤ 1 e pelo círculo x 2 + z 2 ≤ 1   ,     y = 1   .

Passo 1

E aê, gente legal! Tudo belezal? 😊

A questão quer que a gente calcule a integral de superfície para o campo vetorial

F x ,   y ,   z = y   j - z   k

Numa superfície orientada S formada pelo paraboloide

y = x 2 + z 2 ,     0 ≤ y ≤ 1

E pelo círculo

x 2 + z 2 ≤ 1   ,     y = 1

Para isso, temos duas superfícies.

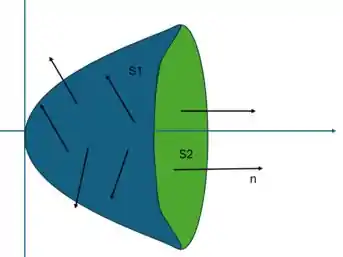
Vamos considerar que S 1 é o paraboloide e S 2 é o disco. Como S é uma superfície fechada, nós usamos a orientação para fora.

Passo 2

Em S 1 , podemos fazer uma representação paramétrica da superfície. Teremos:

r x ,   z = x   i + x 2 + z 2   j + z   k

Para o campo vetorial também:

F r x ,   z = 0   i + x 2 + z 2   j - z   k

Para calcular a superfície, podemos fazer

∫ ∫ S 1   F ∙ d S

Onde

d S = r x × r z d A

Ou seja, o módulo do produto vetorial das derivadas parciais da equação parametrizada que temos acima. Faremos isso:

r x ,   z = x   i + x 2 + z 2   j + z   k

r x = 1 i + 2 x j + 0 k

r z = 0 i + 2 z j + 1 k

Fazendo o produto vetorial:

r x × r z = i j k 1 2 x 0 0 2 z 1 = 2 x   i - j + 2 z   k

Note que a componente em j deve ser negativa em S 1 , para que tenhamos orientação para fora.

Passo 3

Agora, vamos escrever a integral para S 1 e calculá-la:

∫ ∫ S 1   F ∙ d S

Montando, com os limites de integração que está no enunciado:

∬ x 2 + z 2 ≤ 1   0   i + x 2 + z 2   j - z   k ⋅ ( 2 x   i - j + 2 z   k ) d A

Organizando,

∬ x 2 + z 2 ≤ 1   0 ⋅ 2 x + x 2 + z 2 - 1 + - z 2 z   d A

∬ x 2 + z 2 ≤ 1   - x 2 + z 2 - 2 z 2   d A

Como estamos trabalhando com paraboloide e círculo, vamos ter coordenadas polares.

Dessa forma, temos

x 2 + y 2 = r 2

x = r c o s θ ,     y = r s e n θ ,       z = z

d A = r d r d θ

∫ 0 2 π ∫ 0 1 - r 2 - 2 r 2   s e n 2   θ   r   d r   d θ

Dividindo a integral, cada um com seus termos, temos:

∫ 0 2 π - 1 - 2   s e n 2   θ d θ ∫ 0 1 r 3 d r

Resolvendo e substituindo os limites de integração:

- θ - θ - s e n 2 θ 2 0 2 π r 4 4 0 1 = - 4 π 1 4 = - π

Passo 4

Para S 2 , faremos exatamente a mesma coisa:

r x ,   z = x   i + j + z   k   ,               x 2 + z 2 ≤ 1

F r x ,   z = 0   i + j - z   k

As derivadas parciais:

r x = 1   i + 0 j + 0   k

r z = 0 i + 0 j + 1 k

Assim,

r z × r x = i j k 1 0 0 0 0 1 = 0   i + j + 0   k

Então,

∫ ∫ S 2   F ∙ d S

Organizando, temos:

∬ x 2 + z 2 ≤ 1   0 ⋅ 0 + 1 ⋅   1 + - z ⋅   0   d A

∬ x 2 + z 2 ≤ 1   1   d A

Ou seja, calculamos a área do círculo de raio r = 1 , então:

π r 2 = π 1 2 = π

Então, finalmente, temos:

∫ ∫ S   F ⋅ d S = ∫ ∫ S 1   F ⋅ d S + ∫ ∫ S 2   F ⋅ d S = - π + π = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p