Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.7 - Ex. 29

Calcule a integral de superfície ∫ ∫ S   F ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação positiva (para fora).

F x ,   y ,   z = x   i + 2 y   j + 3 z   k  

S é o cubo com vértices ± 1 ,   ± 1 ,   ± 1 .

Passo 1

E aí, galera! Tranquilo?

A questão quer o valor da integral de superfície:

∫ ∫ S   F ∙ d S

Para o campo:

F x ,   y ,   z = x   i + 2 y   j + 3 z   k  

Onde S é o cubo com vértices ± 1 ,   ± 1 ,   ± 1 .

Galera, aqui S consiste de seis superfícies, as seis faces do cubo, conforme mostra a figura:

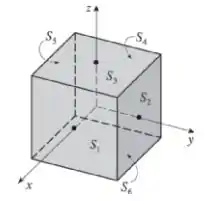
Então, teremos 6 superfícies S . Fazemos o cálculo da integral de superfície para cada uma delas e somamos as 6 no final. O cálculo da integral de superfície é dado pela equação:

∬ S F ⋅ d S = ∬ S F r u , v ⋅ r u × r v d A

Um entendimento que você deve ter é que r u × r v representa o vetor normal (unitário) à superfície. Como estamos tratando de superfícies planas, é relativamente fácil determinar quais são esses vetores normais olhando apenas para a figura.

Passo 2

Para S 1 , vetor normal é o próprio eixo x , ou seja, r u × r v = i = 1,0 , 0 . Além disso, nessa região, você tem seu x sempre valendo 1 enquanto y e z podem variar livremente entre - 1 e 1 . Dessa forma, temos que, nessa região:

F r u , v = 1 ,   2 u ,   3 v

pois substituímos o x por 1 , y por u , onde - 1 ≤ u ≤ 1 e z por v onde - 1 ≤ v ≤ 1 . Nossa integral vai ficar:

∬ S 1 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 1,2 u , 3 v ⋅ 1,0 , 0   d u   d v

Tirando o produto escalar, temos

∬ S 1 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 1 ⋅ 1 + 2 u ⋅ 0 + 3 v ⋅ 0   d u   d v

∬ S 1 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 d u   d v = ∫ - 1 1 d v   ∫ - 1 1 d u

Finalmente,

∬ S 1 F ⋅ d S = 2 ⋅ 2 = 4

Observação: se você achou difícil perceber que   r u × r v = i , você pode tomar a parametrização de S 1 como sendo o plano x = 1 . Assim, a parametrização é:

r u , v = 1 ,   u ,   v

onde - 1 ≤ u ≤ 1 e - 1 ≤ v ≤ 1 . Veja que

r u = 0 ,   1 ,   0

r v = 0,0 , 1

De forma que:

  r u × r v = i j k 0 1 0 0 0 1

  r u × r v = 1 0 0 1 i - 0 0 0 1 j + 0 1 0 0 k = i

Agora é só prosseguir como anteriormente. PORÉM recomendo que você tenha essa interpretação de que r u × r v é o vetor normal, e para casos em que a superfície é plana, é relativamente fácil verificar quem é esse vetor normal apenas analisando a figura. Para os demais casos, vamos fazer sempre assim.

Passo 3

Agora, vamos fazer mais rapidinho para as demais superfícies:

  • Para S 2

    • Observe que o vetor normal está na direção e sentido do eixo y . Assim, temos que r u × r v = j , e além do mais, nessa região y = 1 . Assim, temos que:

    F r u , v = u ,   2 ,   3 v       ;   - 1 ≤ u ≤ 1     ;   - 1 ≤ v ≤ 1

    Dessa forma,

    ∬ S 2 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 u ,   2 ,   3 v ⋅ 0,1 , 0   d u   d v

    ∬ S 2 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 2   d u   d v = 2 ⋅ 2 ⋅ 2 = 8

  • Para S 3

    • Observe que o vetor normal está na direção e sentido do eixo z . Assim, temos que r u × r v = k , e além do mais, nessa região z = 1 . Assim, temos que:

    F r u , v = u , 2 v ,   3   ;   - 1 ≤ u ≤ 1     ;   - 1 ≤ v ≤ 1

    Logo,

    ∬ S 3 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 u , 2 v , 3 ⋅ 0,0 , 1   d u   d v

    ∬ S 3 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 3   d u   d v = 3 ⋅ 2 ⋅ 2 = 12

  • Para S 4

    • Observe que o vetor normal está no sentido negativo de x . Assim, temos que r u × r v = - i , e além do mais, nessa região x = - 1 . Assim, temos que:

    F r u , v = - 1,2 u , 3 v   ;   - 1 ≤ u ≤ 1     ;   - 1 ≤ v ≤ 1

    Logo,

    ∬ S 4 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 - 1,2 u , 3 v ⋅ - 1,0 , 0   d u   d v

    ∬ S 3 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 1   d u   d v = 2 ⋅ 2 = 4

  • Para S 5

    • Observe que o vetor normal está no sentido negativo de y . Assim, temos que r u × r v = - j , e além do mais, nessa região y = - 1 . Assim, temos que:

    F r u , v = u , - 2,3 v   ;   - 1 ≤ u ≤ 1     ;   - 1 ≤ v ≤ 1

    Logo,

    ∬ S 4 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 u , - 2,3 v ⋅ 0 , - 1,0   d u   d v

    ∬ S 3 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 2   d u   d v = 2 ⋅ 2 ⋅ 2 = 8

  • Para S 6

Observe que o vetor normal está no sentido negativo de z . Assim, temos que r u × r v = - k , e além do mais, nessa região z = - 1 . Assim, temos que:

F r u , v = u , 2 v , - 3   ;   - 1 ≤ u ≤ 1     ;   - 1 ≤ v ≤ 1

Logo,

∬ S 4 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 u , 2 v , - 3 ⋅ 0,0 , - 1   d u   d v

∬ S 3 F ⋅ d S = ∫ - 1 1 ∫ - 1 1 3   d u   d v = 3 ⋅ 2 ⋅ 2 = 12

Passo 4

Finalmente, temos:

∬ S F ⋅ d S = ∬ S 1 F ⋅ d S + ∬ S 2 F ⋅ d S + ∬ S 3 F ⋅ d S + ∬ S 4 F ⋅ d S + ∬ S 5 F ⋅ d S + ∬ S 6 F ⋅ d S

∬ S F ⋅ d S = 4 + 8 + 12 + 4 + 8 + 12 = 48

Resposta

48

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p