Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 8
A figuta mostra curvas de nível da função no quadrado . Use a Regra do Ponto Médio com para estimar . Como você melhoraria sua estimativa?
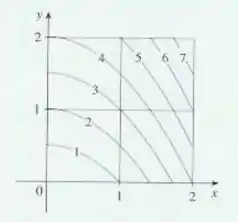
Passo 1
Usando a regra do ponto médio temos que os pontos do intervalo utilizado vai ser o ponto médio de cada intervalo, temos que , vamos calcular , temos que a área total da região é:
Então:
Então usando a soma de Riemann para estimar a integral temos:
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido que está abaixo do paraboloide hiperbólico z = 4 + x 2 - y 2 e acima do quadrado R = - 1 ,1 × 0 ,2 .
Esboce o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 ( 2 - x 2 - y 2 ) d yd x
Encontre o volume do sólido delimitado pelo paraboloide z = 2 + x 2 + y - 2 2 e pelos planos z = 1, x = 1, x = - 1, y = 0 e y = 4 .
Determine o volume do sólido que se encontra abaixo do plano 3 x + 2 y + z = 12 e acima do retângulo R = x ,y0 ≤ x ≤ 1,- 2 ≤ y ≤ 3 }
Desenhe o sólido contido entre as superfícies z = e - x 2 cos x 2 + y 2 e z = 2 - x 2 - y 2 para x ≤ 1,y ≤ 1 . Utilize um sistema de computação algébrica para aproximar o volume desse sólido até a q