Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.7 - Ex. 28

Calcule a integral, transformando para coordenadas cilíndricas.

∫ - 3 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 x 2 + y 2   d z d y d x

Passo 1

Fala pessoal, vamos começar!?

Precisamos calcular a integral abaixo transformando em coordenadas cilíndricas.

∫ - 3 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 x 2 + y 2   d z d y d x

Vamos nessa então!?

Lembre-se antes de tudo, que sempre começamos a integrar de dentro para fora. Nessa situação, vamos começar integrando em d z .

Para transformar em coordenadas cilíndricas, sabemos que:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Para determinar a variação do ângulo e do raio vamos ter que analisar os limites de integração de y e z , e ver a região que é compreendida.

0 ≤ z ≤ 9 - x 2 - y 2

0 ≤ y ≤ 9 - x 2    

Com essas informações, precisamos substituir na integral dada.

Depois é só resolver a integral.

Bora lá!!!

Passo 2

Analisando a integral temos que a região de integração é acima de:

z = 0

e abaixo de:

z = 9 - x 2 - y 2

Agora vamos substituir x e y por coordenadas cilíndricas.

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Substituindo temos:

z = 9 - r 2 cos 2 ⁡ θ - r 2 s e n 2   θ

z = 9 - r 2 ( cos 2 ⁡ θ + s e n 2   θ )

Sabemos da trigonometria que: s e n 2 θ + cos 2 ⁡ θ = 1 .

Logo, nosso intervalo de integração em z é:

0 ≤ z ≤ 9 - r 2

Passo 3

Avaliando o intervalo de integração em y , temos que:

y = 0

y = 9 - x 2

Temos que a segunda expressão descreve uma circunferência de raio 3 , pois podemos escrever a expressão assim:

y 2 = 9 - x 2

y 2 + x 2 = 3 2

Observe como são equivalentes as expressões. Apenas elevamos ambos os lados ao quadrado e deixamos as variáveis de um lado e números do outro.

Mas aqui tem que tomar muito cuidado, pois o ângulo de rotação não vai ser de 0 a 2 π .

Observe a expressão dada em y , ela sempre vai ser positiva independente do valor de x .

y = 9 - x 2

O que isso significa? Que vamos ter meia circunferência! Somente o primeiro e segundo quadrante.

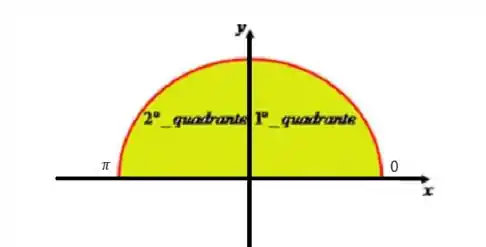
Assim temos que:

0 ≤ r ≤ 3

0 ≤ θ ≤ π

Passo 4

Agora vamos fazer a transformação da integral para coordenadas cilíndricas.

Dos passos anteriores, definimos que nossa região de integração é:

E = r , θ , z | 0 ≤ θ ≤ π ,   0 ≤ r ≤ 3 , 0 ≤ z ≤ 9 - r 2

Em coordenadas cilíndricas temos que:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Temos que substituir na integral a seguir:

∫ - 3 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 x 2 + y 2   d z d y d x

Substituindo vamos ter:

∫ 0 π ∫ 0 3 ∫ 0 9 - r 2 r 2   d z d r d θ

Agora, precisamos resolver essa integral. Lembre-se, começamos a integrar de dentro para fora.

Passo 5

Vamos começar a integrar então.

Integrando em d z , vamos ter:

∫ 0 π ∫ 0 3 r 2 z 0 9 - r 2 d r   d θ

Aplicando os limites de integração, temos:

∫ 0 π ∫ 0 3 9 r 2 - r 4 d r   d θ

Agora vamos integrar em d r .

Integrando, temos:

∫ 0 π 3 r 3 - r 5 5 0 3 d θ

Aplicando os limites de integração, ficamos com:

∫ 0 π 162 5 d θ

Por fim, restou uma integral simples em d θ . Integrando e aplicando os limites de integração temos:

162 5 θ 0 π = 162 π 5

Portando, a resposta da integral em coordenadas cilíndricas é:

∫ - 3 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 x 2 + y 2   d z d y d x = 162 π 5

Resposta

∫ - 3 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 x 2 + y 2   d z d y d x = 162 π 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Converta a integral: ∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 x x 2 + y 2 d z d x d y Em uma integral equivalente em coordenada cilíndricas e calcule o resultado
int_0^(2 pi) int_0^1 int_r^(sqrt(2 - r^2)) d z r d r d theta
Seja D a região delimitada abaixo pelo plano z = 0 , acima pela esfera x 2 + y 2 + z 2 = 4 e dos lados pelo cilindro x 2 + y 2 = 1 . Monte as integrais triplas em coordenadas cilíndricas que fornecem
int_0^2 int_(r - 2)^(sqrt(4 - r^2)) int_0^(2 pi) (r s e n (theta) + 1) r d theta d z d r
int_0^(2 pi) int_0^(pi) int_0^(((1 - cos (varphi))/(2))) rho^2 s e n (varphi) d rho d varphi d theta