Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 42

Calcule a integral, transformando para coordenadas esféricas.

∫ - a a ∫ - a 2 - y 2 a 2 - y 2 ∫ - a 2 - x 2 - y 2 a 2 - x 2 - y 2 ( x 2 z + y 2 z + z 3 )   d z   d x   d y

Passo 1

E aiiiiii turminha, tudo bem?! Vamos nessa!

Nosso objetivo é calcular a integral abaixo a partir da sua transformação em coordenadas esféricas:

∫ - a a ∫ - a 2 - y 2 a 2 - y 2 ∫ - a 2 - x 2 - y 2 a 2 - x 2 - y 2 ( x 2 z + y 2 z + z 3 )   d z   d x   d y

Como começamos essa!?

Primeiro vamos recordar das coordenadas esféricas. Temos o seguinte:

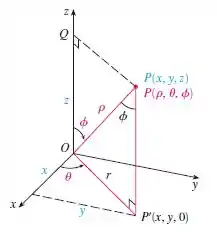
Lembre-se que em coordenadas esféricas o d V = d x d y d z , fica:

d V =   ρ 2 sin ⁡ ϕ d ρ   d ϕ   d θ

Agora observe os limites de integração da integral dada, e note que z varia da parte inferior da esfera de raio a até a parte superior:

- a 2 - x 2 - y 2 ≤ z ≤ a 2 - x 2 - y 2

De modo que podemos fazer a restrição ρ ≤ a .

No plano x y , y varia de - a até a , enquanto x vai da parte inferior da circunferência de raio a até a superior.

Logo, o domínio de integração é claramente limitado pela esfera x 2 + y 2 + z 2 = a 2 .

Assim, temos:

0 ≤ ρ ≤ a

0 ≤ θ ≤ 2 π

0 ≤ ϕ ≤ π

Já sabemos os intervalos de integração. Agora devemos substituir x, y e z da expressão:

( x 2 z + y 2 z + z 3 )

pelos respectivos termos em coordenadas esféricas. Depois, é só resolver a integral.

Bora lá!!!

Passo 2

Vamos escrever a integral em coordenadas esféricas:

∫ - a a ∫ - a 2 - y 2 a 2 - y 2 ∫ - a 2 - x 2 - y 2 a 2 - x 2 - y 2 ( x 2 z + y 2 z + z 3 )   d z   d x   d y

Em coordenadas esféricas, sabemos que:

x = ρ sin ⁡ ϕ cos ⁡ ( θ )

y = ρ sin ⁡ ϕ sen ⁡ ( θ )

z = ρ cos ⁡ ϕ

E os intervalos são:

0 ≤ ρ ≤ a

0 ≤ θ ≤ 2 π

0 ≤ ϕ ≤ π

Agora, vamos olhar para o integrando

( x 2 z + y 2 z + z 3 )

Em coordenadas esféricas, temos que:

x 2 z + y 2 z + z 3 = ρ cos ⁡ ϕ ρ 2 = ρ 3 cos ⁡ ϕ

Portanto, substituindo na integral temos:

∫ 0 a ∫ 0 2 π ∫ 0 π ρ 3 cos ⁡ ϕ ρ 2   s e n   ϕ   d ϕ d θ d ρ

Passo 3

Agora devemos resolver a integral:

∫ 0 a ∫ 0 2 π ∫ 0 π ρ 5 cos ⁡ ϕ   s e n   ϕ   d ϕ d θ d ρ

Lembre-se, devemos começar integrando de dentro para fora.

Integrando em d ϕ vamos ter que fazer uma substituição do tipo:

u = s e n   ϕ

d u = cos ⁡ ϕ   d ϕ

Substituindo, temos que:

∫ 0 a ∫ 0 2 π ∫ 0 π ρ 5 u   d u d θ d ρ

Vamos integrar em d u , e depois voltamos para a variável ϕ . Um ponto importante, tudo que não depende da variável ϕ consideramos uma constante.

Assim, integrando temos:

∫ 0 a ∫ 0 2 π ρ 5 ( s e n   ϕ ) 2 2 0 π d θ d ρ

Substituindo os intervalos de integração temos:

∫ 0 a ∫ 0 2 π ρ 5 ( s e n   π ) 2 - ( s e n   0 ) 2 2 d θ d ρ

Como:

s e n   π = 0

s e n   0 = 0

Temos:

∫ 0 a ∫ 0 2 π ρ 5 0 - 0 2 d θ d ρ

∫ 0 a ∫ 0 2 π ( 0 ) d θ d ρ

Podemos parar por aqui, porque vai dar zero nossa integral.

Assim, nossa resposta é:

∫ - a a ∫ - a 2 - y 2 a 2 - y 2 ∫ - a 2 - x 2 - y 2 a 2 - x 2 - y 2 ( x 2 z + y 2 z + z 3 )   d z   d x   d y = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o sólido descrito pelas desigualdades dadas. ρ ≤ 2 , ρ ≤ c o s s e c ( ϕ )
Um sólido está acima do cone z = x 2 + y 2 e abaixo da esfera x 2 + y 2 + z 2 = z . Escreva uma descrição do sólido em termos de desigualdades envolvendo coordenadas esféricas.
Determine o volume da menor cunha esférica cortada de uma esfera de raio a por dois planos que se interceptam ao longo de um diâmetro com um ângulo de π / 6 .
Utilize as coordenadas esféricas.Encontre a distância média de um ponto em uma bola de raio a e seu centro.
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada.Determine o volume e o centroide do sólido E que está acima do cone z = x 2 + y 2 e abaixo da esfera x 2 + y 2