Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 14
Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
Olá, tudo bem?
A questão quer que a gente esboce o sólido que é descrito por:
Bom, como temos uma região em função de , o que temos aqui é uma região descrita em coordenadas esféricas.
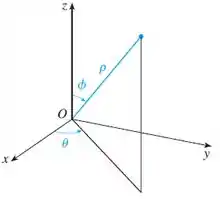
Esquema de representação de um ponto em coordenadas esféricas
Então, vamos analisar variável por variável, achar o comportamento de cada uma e entender qual sólido cada uma dessas variações vão formar.
Vamo que vamo!
Passo 2
Sabemos das coordenadas esféricas que é uma esfera centrada na origem e de raio . Então o sólido é uma esfera sólida de raio .
Mas acabou? Não! Devemos dar uma olhada no ângulo .
O ângulo satisfaz a seguinte desigualdade:
Como:
Substituímos:
Isolando seno:
Então o ângulo começa lá em cima e vai até onde é , que é em
Então é só uma porção superior de um sorvete, até .
Por enquanto é isso pessoal, espero ter ajudado ;)
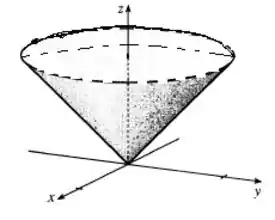
Resposta
