Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 1d

Calcule a integral tripla:

∭ W y cos ⁡ x + z   d x d y d z

Onde W é a região limitada pelo cilindro x = y 2 e os planos x + z = π 2 e z = 0 .

Passo 1

Este exercício é bem interessante porque ele fala de cilindro mas não existe cilindro nenhum. Existe uma parábola ao longo de todo o eixo z. Mas tudo bem hahaahaha

Vamos trabalhar com a projeção disso no plano x y ; obteremos o seguinte:

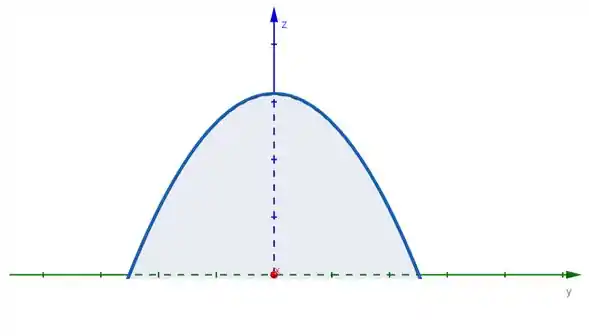
Sempre buscamos trabalhar com as projeções. Não esquece disso.

Se você não conseguiu visualizar isso, podemos invocar a tia Mat; substituindo o x = y 2 na fórmula do plano:

y 2 + z = π 2

Portanto:

z = π 2 - y 2

Que é exatamente essa parábola, voltada pra baixo com origem em z = π 2 . Linda como sempre.

Passo 2

Bom, vamos tentar achar os limites de integração:

Olhando em y subindo no sentido do eixo z a única coisa que encontramos é a parábola voltada para baixo; então:

0 ≤ z ≤ π 2 - y 2

Agora perceba que os pontos em que a parábola corta o eixo y são justamente os limites:

- π 2 ≤ y ≤ π 2

Por ultimo o tiozinho x , caminhando do plano y z no sentido de positivo de x , primeiro batemos de frente com o cilindro e seguindo mais adiante encontramos o plano que corta esse cilindro; portanto:

y 2 ≤ x ≤ π 2 - z

Prestando bem atenção à ordem em que vamos realizar a integração.

Passo 3

Vamos ter que trabalhar com a seguinte integral:

I = ∫ - π 2 π 2 ∫ 0 π 2 - y 2 ∫ y 2 π 2 - z y cos ⁡ x + z d x   d z   d y

Aquela soma no meio do cosseno assusta um pouco, mas se você chamar aquilo ali de u , vai ver que é só integrar normal; sem neuras:

V = ∫ - π 2 π 2 ∫ 0 π 2 - y 2 y [ sin ⁡ x + z ]   d z   d y x = π 2 - z x = y 2

E aí:

V = ∫ - π 2 π 2 ∫ 0 π 2 - y 2 y [ sin ⁡ π 2 - z + z - sin ⁡ y 2 + z ]   d z   d y

V = ∫ - π 2 π 2 ∫ 0 π 2 - y 2 y 1 - sin ⁡ y 2 + z d z   d y

A próxima:

V = ∫ - π 2 π 2 ∫ 0 π 2 - y 2 y - y sin ⁡ y 2 + z d z   d y

V = ∫ - π 2 π 2 y z - y cos ⁡ y 2 + z d y z = π 2 - y 2 z = 0

Ajeitando isso:

V = ∫ - π 2 π 2 y π 2 - y 2 - y cos ⁡ y 2 + π 2 - y 2 - cos ⁡ y 2 d y

Horrível... Mas temos que olhar com muito cuidado pra não errar os sinais:

V = ∫ - π 2 π 2 π 2 y - y 3 + y cos ⁡ y 2 d y

Ééééé... Bais ou benos... Ta melhorzinho vai.

Uma dica rapidona, chama u = y 2 portanto d u = 2 y   d y . Certo??

Então a integral desse termo:

∫ y cos ⁡ y 2 d y = ∫ d u 2 cos ⁡ ( u ) = 1 2 ∫ cos ⁡ ( u ) d u = sin ⁡ u 2 = sin ⁡ y 2 2

Tá comigo?? Então vamo:

V = π 4 y 2 - y 4 4 + sin ⁡ y 2 2 y = π 2 y = - π 2

Aplicando esses limites, perceba que todos os expoentes em y são pares, então o sinal negativo do limite inferior já vai passear; e com isso tudo zera:

V = π 4 π 2 2 - π 2 2 - π 2 4 - π 2 4 4 + sin ⁡ π 2 2 - sin ⁡ π 2 2 2 = 0

É pra ficar feliz ou puto? Fica a reflexão... inté mais!

Resposta

Portanto, depois de um trabalho judioso, encontramos que o volume do cujo dito sólido é ZERO.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ 0 2 d x ∫ 0 2 x - x 2 d y ∫ 0 a z x 2 + y 2 d z .
W = x , y , z ∈ R 3 x 2 + y 2 + z 2 ≤ a 2ez 2 ≤ x 2 + y 2 .
Calcule a seguinte integral tripla: ∭ W x y 2 z 3d x d y d z Onde W é a região no primeiro octante limitada pela superfície z = x y e os planos y = x ,x = 1 e z = 0 .
Calcule a seguinte integral tripla: ∭ W zd x d y d z Onde W é a região limitada pelas superfícies z = x 2 + y 2 ,y = x 2 ,z = 0ey = 1 .