Calcule a seguinte integral tripla:
Onde é a região limitada pelas superfícies .
Passo 1
Vocês estão prontas crianças?? Hôôôôôôô....
Faaalaa marujo, vamos de mais integral tripla.
Como nesse exercício já temos a integral, não precisa ficar se matando tentando desenhar o esboço 3D dele.
Vamos precisar somente das projeções para definir os limites dessa integral.
Projetando isso no plano , teremos algo mais ou menos assim:
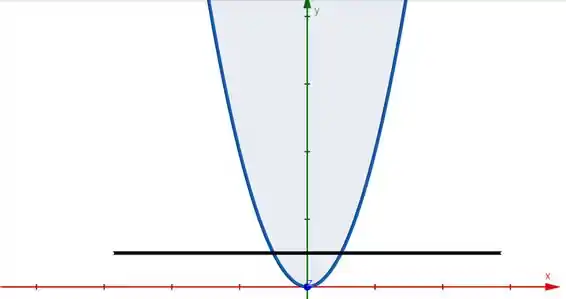
Pegou a idéia?
Passo 2
Com isso, podemos tentar identificar os limites de integração.
Consegue perceber que:
Enquanto que se sairmos da origem no sentido positivo de encontramos primeiro a parábola e depois damos de cara com a reta ; portanto:
Agora vamos dar uma olhada em , se descolarmos do plano mais cedo ou mais tarde vamos dar de frente com o cone:
Então show debola, estamos com os três limites da integral.
Passo 3
Teremos o seguinte:
Lembrando sempre da ordenação das integrais e dos decimais, de dentro pra fora.
Então vamos começar:
Seguindo:
Vamos dividir em duas partes pra não confundir os bois:
Portanto:
E finalmente:
Chegamos em:
Quase acabando, a segunda integral:
Let’s bora:
Agora o :
Chegamos em:
Cuidado com a ansiedade, essa ainda não é a resposta:
É isso! Até mais!!
Resposta
A solução para a integral dada é: