Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 2f
Passo 1
Nos encontramos aqui novamente, vão bora!!
Queremos calcular o volume desse sólido, mas que sólido é esse?!
Ao utilizarmos as equações, podemos ver que temos algo como a junção de uma esfera e um cone, algo parecido como:
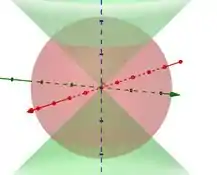
A equação é referente a esfera em vermelho e a equação é referente ao cone em verde.
Passo 2
Beleza, para calcular o volume do sólido vamos resolver uma integral tripla do tipo:
Temos, porém, um sólido esférico, daí, vamos realizar uma mudança de variáveis para coordenadas esféricas, lembrando que:
E seu jacobiano sendo dado por .
Assim,
Passo 3
Vamos agora analisar os intervalos de integração. Temos que estará compreendido entre , pois ele está se referindo a uma distância de um ponto P da superfície da esfera até a sua origem.
Note agora a que e se referem na figura abaixo:
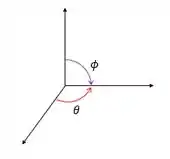
Assim, para o sólido que temos, a variação em será de , pois haverá uma rotação completa em torno do eixo y.
Já para a variação de , vamos precisar saber da interseção das duas formas, assim:
Daí,
Ou seja,
Temos que
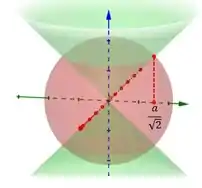
Nas mudanças de variáveis, teremos que , assim:
Ou seja, como é a variação do ângulo a partir do eixo y, teremos:
Passo 4
Resolvendo a integral, teremos que o volume do sólido será dado por:
Note que utilizamos só a parte superior da esfera, pois estamos tratando com o intervalo de referente a ela, logo, ao multiplicar o resultado da integral por 2, teríamos a outra metade da esfera, assim:
Resposta
O volume do sólido é dado por: .