Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 1b

Calcule a seguinte integral tripla:

∭ W x y 2 z 3   d x d y d z

Onde W é a região no primeiro octante limitada pela superfície z = x y   e os planos y = x ,   x = 1     e     z = 0 .

Passo 1

Faalaa carinha... Esse exercício é meio estranho, vem comigo!

Antes de mais nada vamos tentar enxergar o que acontece nesse role:

Não faz a menor ideia de como esboçar essa curva né?! Pois é... eu também não.

Mas uma saída seria olharmos para a projeção disso tudo no plano x y . Lembrando que temos as seguintes retas:

y = x       e       x = 1

Então teremos algo assim:

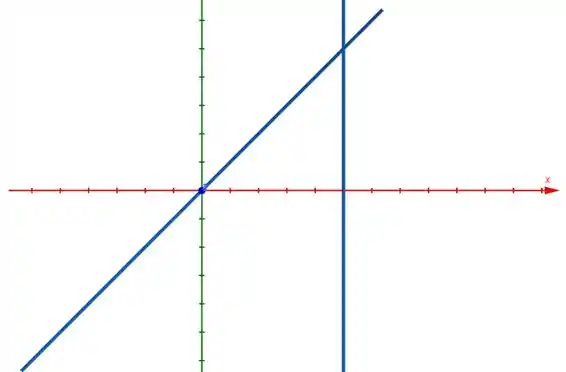
Passo 2

Bom, já temos alguma coisa né?!

Vamos ver se encontramos os limites das integrais:

Saindo da origem, no sentido positivo do eixo x :

0 ≤ x ≤ 1

Saindo de um ponto entre 0 e 1 no eixo x , subindo no sentido positivo de y vamos dar de cara com a reta y = x ; ou seja:

0 ≤ y ≤ x

Agora e o z   ?? que diaxo vamos fazer com esse cara??

Bom, a gente não sabe exatamente como a curva se comporta né? Mas tudo indica que se sairmos do plano x y e subirmos na direção positiva de z vamos nos deparar com a tal curva, então:

0 ≤ z ≤ x y

Passo 3

Portanto vamos ter a seguinte integral:

I = ∫ 0 1 ∫ 0 x ∫ 0 x y x y 2 z 3   d z d y d x

É só integrar então:

I = ∫ 0 1 ∫ 0 x x y 2 z 4 4   d y d x z = x y z = 0

Ficaremos com:

I = 1 4 ∫ 0 1 ∫ 0 x x y 2 x 4 y 4 d y d x

Seguimos:

I = 1 4 ∫ 0 ; 1 x 5 y 7 7 d x y = x y = 0

E finalmente:

I = 1 28 ∫ 0 1 x 12 d x = 1 28 x 13 13 x = 1 x = 0  

Ou seja:

I = 1 364

That’s all...

Resposta

Concluimos que:

∭ W x y 2 z 3   d x d y d z = 1 364

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a seguinte integral tripla: ∭ W zd xd yd x Onde, W é a região no primeiro octante limitada pelos planos y = 0 , z = 0 , x + y = 2 , 2 y + x = 6 e o cilindro y 2 + z 2 = 4 .
Calcule o volume do sólido W descrito abaixo. W é limitado pelo cone z = x 2 + y 2 e o parabolóide z = x 2 + y 2 .
Calcule o volume do sólido W descrito abaixo:(b) W é limitado pelas superfícies z = 8 - x 2 - y 2 e z = x 2 + 3 y 2 .
Calcule o volume do sólido W descrito abaixo:(e) W = x , y , z ∈ R 3 z ≥ 1;x + y + z ≤ 7;x ≥ y 2 .
Calcule o volume do sólido W descrito abaixo.(c) W é limitado pelas superfícies z = 4 - x 2 - y 2 e z = y , está situado no interior do cilindro x 2 + y 2 = 1 , e z ≥ 0 .