Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 53

Calcule a integral trocando a ordem de integração.

∫ 0 1   ∫ x 1 y 3 + 1 d y d x

Passo 1

E aí, galera! Tudo joia?

A questão quer o cálculo de:

∫ 0 1   ∫ x 1 y 3 + 1 d y d x

Porém, com outra ordem de integração.

Aqui no nosso caso vamos ter que manipular nossos limites de integração da região de integração de forma que a integral de d x fique “pra dentro”.

Então, vamos precisar do gráfico da região D para fazer essa modificação.

Vamos ver como fica passo a passo!

Passo 2

Olhando os limites de integração das integrais vemos que:

0 ≤ x ≤ 1

x ≤ y ≤ 1

O primeiro passo é esboçar a região:

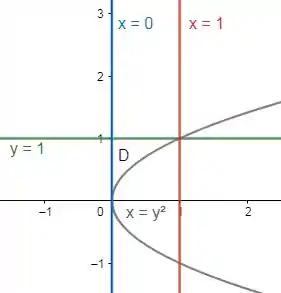
Invertendo a ordem de integração, vamos achar uma forma de expressar o intervalo de y entre duas constantes e o de x entre duas funções.

Assim temos que x vai de 0 até y 2 , enquanto y vai do eixo x ( y = 0 ) até a reta y = 1 . Assim:

∫ 0 1   ∫ x 1 y 3 + 1 d y d x = ∫ 0 1   ∫ 0 y 2 y 3 + 1 d x d y

Passo 3

Resolvendo a integral de dentro, temos:

∫ 0 y 2 y 3 + 1 d x = y 3 + 1 x 0 y 2

∫ 0 y 2 y 3 + 1 d x = y 2 y 3 + 1

Portanto:

∫ 0 1   ∫ 0 y 2 y 3 + 1 d x d y = ∫ 0 1   y 2 y 3 + 1 d y

Vamos aplicar a integração por substituição:

Seja:

u = y 3 + 1  

d u = 3 y 2 d y

y 2 d y = d u 3

Analisando os limites, temos:

y = 0 → u = 1

y = 1 → u = 2

Substituindo, temos:

∫ 0 1   y 2 y 3 + 1 d y = ∫ 1 2   u d u 3

∫ 1 2   u d u 3 = 1 3 u 3 2 3 2 1 2

∫ 1 2   u d u 3 = 2 9 2 3 / 2 - 1

∫ 1 2   u d u 3 = 2 9 2 2 - 1

A nossa resposta será:

∫ 0 1   ∫ 0 y 2 y 3 + 1 d x d y = 2 9 2 2 - 1

Resposta

∫ 0 1   ∫ 0 y 2 y 3 + 1 d x d y = 2 9 2 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse D com a união de regiões do tipo I ou do tipo I I e calcule a integral. ∬ D x 2 d A
Expresse D com a união de regiões do tipo I ou do tipo I I e calcule a integral. ∬ D y d A
Calcule a integral trocando a ordem de integração. ∫ 0 2∫ y 2 1 y cos ⁡ x 3 - 1 d x d y
Esboce a região de integração e mude a ordem de integração. ∫ - 2 2 ∫ 0 4 - y 2 f x , y d x d y