Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 46
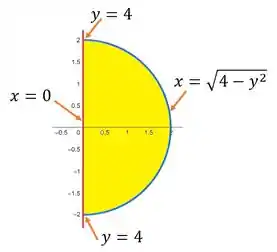
Esboce a região de integração e mude a ordem de integração.
Passo 1
Faaala turminha!? Bora lá!!
O enunciado pede para esboçar a região de integração e mudar a ordem de integração da seguinte integral:
Como faço isso?
Primeiro vamos lembrar de integral de região do tipo I e tipo II.
A região do tipo I é uma região limitada acima e abaixo por uma curva, e limitada lateralmente por retas verticais.
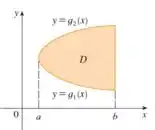
Já uma região do tipo II é o contrário. É uma região limitada lateralmente por curvas, mas acima e abaixo por retas horizontais.
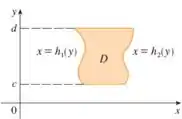
Devemos primeiro fazer o esboço da região. Com essas informações acima, de região tipo I e II, devemos identificar qual é o tipo de região da integral fornecida. Com isso, podemos fazer a mudança para o outro tipo de região.
Bora colocar mão na massa!
Passo 2
De início, vamos focar em identificar nossa região. Compare a integral fornecida com as do tipo I e II.
Como estamos integrando inicialmente em , significa que estamos trabalhando com uma região do tipo II.
O domínio da mesma é:
Agora que determinarmos a nossa região, podemos esboça-la. Utilizando o Geogebra obtemos:
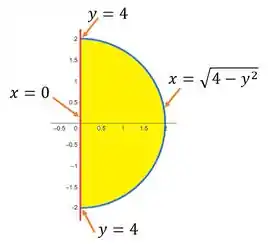
Onde a região de interesse, e a área em amarelo. Observe que ela está delimitada pelo domínio que escrevemos acima.
Passo 3
Esboçamos a região de integração, e sabemos que ela é do tipo II. Vamos escrevê-la como uma região do tipo I.
Veja a imagem da região novamnete:
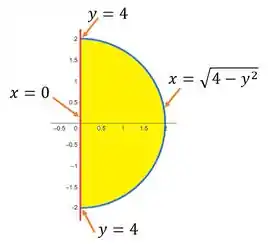
Observe que precisamos escrever em função de :
Portanto, a região é limitada à esquerda pela reta , à direita pela reta , acima pela curva e abaixo pela curva .
Logo, a integral correspondente é dada por:
Resposta
