Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 58

Expresse D com a união de regiões do tipo I ou do tipo I I e calcule a integral.

∬ D y d A

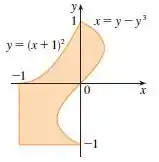
Passo 1

A questão pede par escrevermos a integral sobre a região dada e em seguida calculá-la.

Como é muito difícil inverter a equação x = y - y 3 para escrever y como função de x , teremos que fazer a integração na ordem d A = d x d y . Para isso, vamos precisar quebrar a integral em duas partes, uma com y ≤ 0 e outra com y ≥ 0 . Para a integral acima do eixo x , temos que x vai da curva y = x + 1 2 até x = y - y 3 . Invertendo a primeira equação:

x = - 1 + y

Portanto:

∫ 0 1   ∫ - 1 + y y - y 3 y d x d y

Já para a região abaixo do eixo x , x varia de x = - 1 até x = y - y 3 . Portanto:

∫ - 1 0   ∫ - 1 y - y 3 y d x d y

Desta forma, temos que:

∬ D y d A = ∫ 0 1   ∫ - 1 + y y - y 3 y d x d y + ∫ - 1 0   ∫ - 1 y - y 3 y d x d y

Passo 2

Resolvendo as integrais de dentro, temos:

∬ D y d A = ∫ 0 1   y y - y 3 + 1 - y d y + ∫ - 1 0   y y - y 3 + 1 d y

∬ D y d A = ∫ 0 1   y 2 - y 4 + y - y y d y + ∫ - 1 0   y 2 - y 4 + y d y

Note que podemos juntar as partes dos integrandos que são iguais em uma só integral:

∬ D y d A = ∫ - 1 1   y 2 - y 4 + y d y - ∫ 0 1   y 3 / 2 d y

Como y é impar e y 2 e y 4 são pares, temos que:

∬ D y d A = 2 ∫ 0 1   y 2 - y 4 d y - ∫ 0 1   y 3 / 2 d y

Portanto:

∬ D y d A = 2 y 3 3 - y 5 5 0 1 - 2 5 y 5 2 0 1

∬ D y d A = 2 3 - 2 5 - 2 5 = - 2 15

A nossa resposta será:

∬ D y d A = - 2 15

Resposta

∬ D y d A = - 2 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1∫ a r c t gx π 4 f ( x , y ) d y d x
Esboce a região de integração e mude a ordem de integração. ∫ 1 2∫ 0 ln ⁡ x f ( x , y ) d y d x
Calcule a integral trocando a ordem de integração. ∫ 0 1∫ 3 y 3 e x 2 d x d y
Calcule a integral trocando a ordem de integração. ∫ 0 1∫ x 2 1 y sin ⁡ y d y d x
Calcule a integral trocando a ordem de integração. ∫ 0 8∫ y 3 2 e x 4 d x d y