Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 57
Expresse com a união de regiões do tipo ou do tipo e calcule a integral.
Passo 1
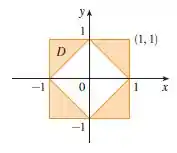
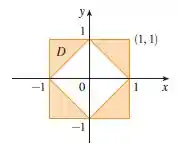Vamos lá meu amigo! Veja que temos uma figura com um formato um pouco não tão usual. Por isso, a melhor forma de resolver a integral dupla mencionar é pensarmos no teorema fundamental do cálculo, que diz que eu posso resolver uma integral de uma região e depois somar o resultado. Veja a figura:
Neste caso, vamos quebrar a integral em quatro partes, uma em cada quadrante, pois assim ficará mais fácil definir os limites de integração. Uma vez definido os limites de integração podemos calcular a integral:
Além disso, note que o integrando é uma função par, e a região de integração é simétrica. Desta forma, podemos calcular a integral apenas sobre a região e multiplicar o resultado por .
Passo 2
No primeiro quadrante, temos que varia de a , enquanto vai de até :
Veja que nossa integral é do tipo , pois ela vai “varrendo” a região da parte inferior até a parte superior.
Já no quarto quadrante, varia de até . Assim:
Desta forma, temos que:
Passo 3
Resolvendo as integrais de dentro, temos:
Portanto:
Agora é só resolver:
A nossa resposta será: