Calcule a integral usando integração por partes tabulada.

Podemos resolver o exercício utilizando Integração por partes tabulada, que consiste em derivar repetidamente uma das funções (geralmente o polinômio) até chegar em zero.

Após derivar repetidamente os termos, iremos traçar uma seta partindo da primeira entrada da coluna de derivação, até o ponto da coluna de integração na linha de baixo, e faremos isso até atingir o último termo e identificaremos com sinais ... iniciando sempre com o sinal positivo. Bora lá?

Começando com a derivação repetida e integração repetida:

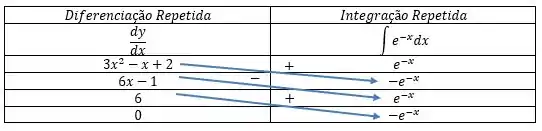
Agora, vamos considerar os favores interligados pela seta, como uma multiplicação, inclusive de sinais. Dessa forma:

Assim:

Multiplicando os termos, temos:

Reorganizando, temos:

Calculando, temos:

Retirando o sinal de dentro da fórmula: