Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.2 - Ex. 1a
Calcule
Passo 1
Fala, galera! Tudo bem? Vamos resolver essa questão!
O enunciado pediu pra gente calcular o limite da função quando tende a infinito.
Para calcular limites infinitos precisamos dar uma olhada na função. Temos aqui um polinômio de ordem , que é o nosso . Então, vamos analisar o que acontece quando tende a valores infinitamente grandes e verificar o comportamento da nossa função.
Vamos lá!
Passo 2
Então vê comigo, se como o enunciado falou, imagina pegar um número gigantesco e elevar ele a ? Só pra você ter uma ideia:
O volume de um tanque desses elevado a quarta potência dá algo equivalente a pouco mais de piscinas olímpicas em volume:
Ok mas pra quê isso? Bem, veja que o volume é uma grandeza positiva e, se elevada a quarta potência, continua assim! De forma geral:
Se olharmos pra função como:
Quem você acha que ganha lá no infinito? O volume de piscinas olímpicas ou de aproximadamente três containers? Isso significa que, nesse caso, quem define o comportamento da função é o termo . Assim, vemos que esse limite será:
Passo 3
Só pra aproveitar a reflexão galera, e generalizar. Isso vai servir pra quem gosta mais de pegar a manhã pelo padrão, mas se você é mais de ver caso a caso, nem se preocupa com esse passo! Seja qualquer polinômio de ordem , temos:
Onde
Então, vamos ter:
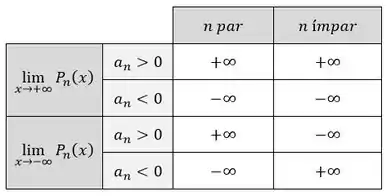
E tá aí a explicação mais gen��rica.
Valeu, galera! Até a próxima! 😉