Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.1 - Ex. 4
Calcule:
Mostre que existe tal que
Passo 1
Para resolver a letra precisamos dividir todos os termos (tanto do numerador, quanto do denominador) pelo de maior expoente, que no nosso caso é .
Sendo assim, dividindo todos os termos por temos:
Agora simplificando temos:
Agora vamos analisar o comportamento desse limite. Quando , os denominadores de (), ficam cada vez maiores, e o resultado dessa divisão tende a zero.
Então temos para cada um dos termos:
Daí temos que no numerador, todos os termos tendem a zero. E no denominador, apenas sobrevive o :
Conlcuindo: o resultado desse limite é zero!
Beleza? Vamos pra próximo item?
Passo 2
Agora vamos analisar a parte da esquerda dessa desigualdade:
Do numerador temos:
E do denominador:
Com a ajuda de um programa de gerar gráficos temos:
Então essa função só é positiva para . Então combinando os resutlados:
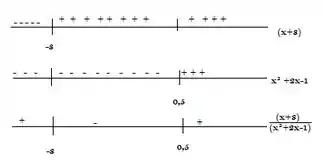
Mas procuramos por valores positivos, uma vez que e que . Sendo assim o intervalo de interesse é .
Passo 3
Agora vamos olhar para o outro lado da desigualdade:
Com a ajuda de um programa de geração gráfica temos:
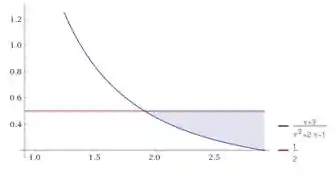
A razão vai ser menor do que a partir do ponto onde eles se encontram em diante. O ponto onde eles se encontram é:
Multiplicando cruzado temos:
Então:
E o intervalo de interesse aqui é . Combinando isso com o outro intervalo (lembrando que deve satisfazer os dois intervalos ao mesmo tempo) temos como resposta: . Então existe sim tal que
E nesse caso . Beleza?