Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.3 - Ex. 28
Calcule o limite, se ele existir.
Passo 1
Iremos analisar o seguinte limite:
Primeiro passo, já sabe né, substitui o valor do limite para ver no que dá:
Opa, tivemos aqui uma indeterminação do tipo .
Para conseguir retira-la, iremos fatorar o numerador e o denominador.
No numerador podemos reparar que temos o seguinte produto notável ocorrendo:
Onde e
Já no denominador temos um polinômio de quarto grau... o que pode ser um pouquinho complicado, mas tem erro não. Para fatorá-lo, vamos fazer divisão de polinômios.
Sabemos que é uma raíz do polinômio do denominador (afinal ele zera quando ), dessa forma, podemos fatora-lo fazendo:
E para encontrar esse polinômio basta dividir por .
Vamos fazer tudo isso nós passos seguintes, bora lá?!
Passo 2
Inicialmente, vamos fatorar o polinômio do numerador, fazendo:
Aplicando no nosso numerador, ficamos com:
Perfeito, então nosso limite fica sendo:
Show de bolê... vamos para o denominador agora...
Passo 3
Para o denominador, iremos dividi-lo por (pois sabemos que é uma de suas raízes).
Realizando a divisão de polinômios, obtemos:
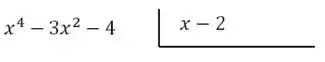
Daí devemos fazer dividido por resulta em :
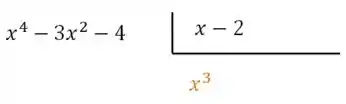
multiplicado por resulta em que deve ir com sinal trocado pro outro lado:
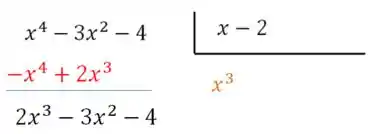
Então realizando a operação , obtemos:
E agora repetimos a operação. dividido por resulta em :
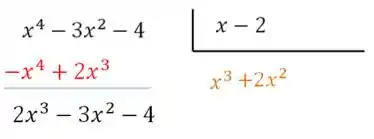
E multiplicado por resulta em que vai pro outro lado com sinal trocado e então realizando a soma obtemos:
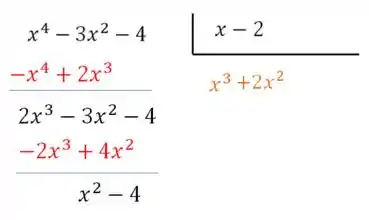
Acho que você já entendeu a ideia... aí é só repetir até chegar no resto zero
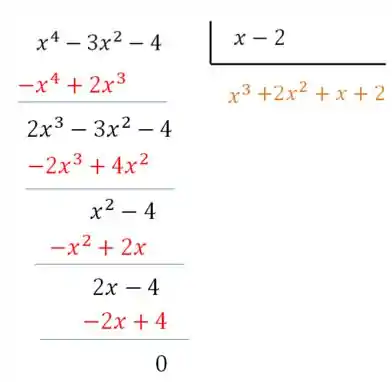
Dessa forma, podemos dizer que:
E como queríamos fatorar o polinômio de quarto grau, podemos por fim dizer que:
Agora é só substituir isso no limite
Passo 4
Tínhamos que
E fatoramos o denominador obtendo:
Perfeito, temos um em cima que podemos cortar com um embaixo!
Essa operação deve ter sido suficiente para retirar a indeterminação, vamos então substituir o valor do limite:
Show de bolê!!