Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 2
Calcule a soma de Riemann para , , com seis subintervalos, tomando os pontos amostrais como as extremidades direitas. O que representa a soma de Riemann? Ilustre com um diagrama.
Passo 1
Opa! E aí, bora resolver essa questão?! O enunciado pede pra a gente calcular a soma de Riemann para essa função aqui:
No intervalo . Ou seja, queremos calcular:
O próprio enunciado já diz que a gente deve resolver o problema pela soma de Riemann, pra isso a gente vai usar essa forma geral aqui:
Onde é dado por:
Como a gente vai pegar os pontos da extremidade direita de cada intervalo, para achar cada ponto fazemos:
Pro nosso caso teremos:
Na prática, pra fazer o exercício, vamos abrir a integral ali de cima e vamos ficar com:
Passo 2
Substituindo e calculando:
Lembrando que:
Temos então:
Assim:
E resolvendo, ficamos com:
Passo 3
Agora a gente vai tentar entender, geometricamente o que fizemos nesse exercício!
A nossa função é no intervalo , se esboçarmos essa curva, teremos:
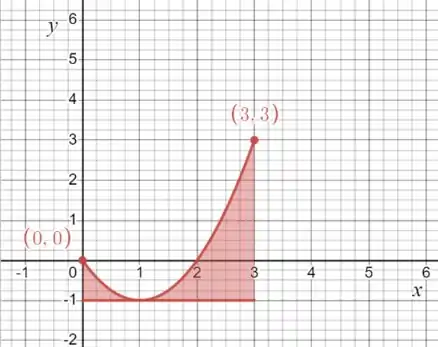
A integral de nesse intervalo é a área dessa região pintada de vermelho!
Na soma de Riemann a gente dividiu esse intervalo de em pedacinhos e calculamos . Essa multiplicação te lembra alguma coisa?! O que fizemos pra cada intervalo foi:
Ou seja, calculamos a área desses retângulos e isso nos dá o valor aproximado da integral. Se a gente desenhar o que fizemos, vamos ter isso daqui:
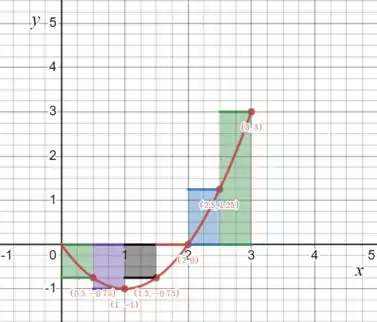
Repara que a “altura” é sempre o ponto mais a direita de cada intervalo, como o enunciado pediu.
Agora, você concorda comigo que quanto menor for a largura do retângulo e mais retângulos tivermos, mais precisa vai ser a nossa conta. E que quando tende a infinito a gente tem o valor exato da integral?!
Esse é o espirito da coisa!