Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.3 - Ex. 74

  1. Calcule ∫ x x 2 + 1 d x .
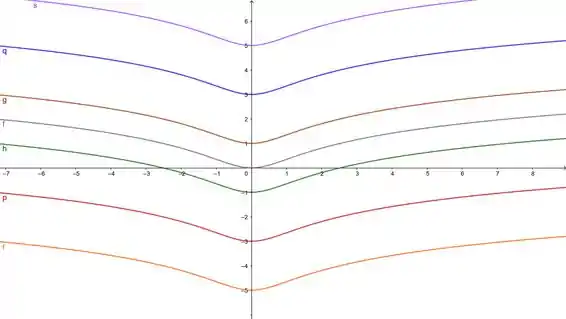
  2. Use um recurso gráfico para gerar algumas curvas integrais típicas de f x = x x 2 + 1   sobre o intervalo - 5,5 .

Passo 1

  1. Vamos calcular a integral pedida:

∫ x x 2 + 1 d x

Aqui a gente vai jogar uma substituição assim:

u = x 2 + 1

d u = 2 x   d x → d u 2 = x   d x

Aí fica:

1 2 ∫ d u u

Integrando fica:

1 2 ln ⁡ u + C

A gente volta pra x :

1 2 ln ⁡ ( x 2 + 1 ) + C

E foi!

Passo 2

Curvas integrais são os gráficos do resultado da integral. Veja que 1 2 ln ⁡ x 2 + 1 + C

gera uma família de curvas, conforme vai variando o C . Vamos fazer algumas então no intervalo pedido:

Resposta

  1. 1 2 ln ⁡ x 2 + 1 + C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 33 a 44, calcule a integral definida.39. ∫ π 6 π 3 3 d x 2 s e n2 x + 1
Nos exercícios de 33 a 44, calcule a integral definida.38. ∫ 0 π 2 d x 3 + c o s 2 x
Calcule ∫ 2t gx 2 + 3 cos ⁡ xd x
g) ∫ c o s s e c n x d x = - c o s s e c n - 2 x ⋅ c o t g x n - 1 + n - 2 n - 1 ⋅ ∫ c o s s e c n - 2 x d x , n ≥ 2
Calcule ∫ c o t g n x d x = - c o t g n - 1 x n - 1 - ∫ c o t g n - 2 x d x