Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 31b
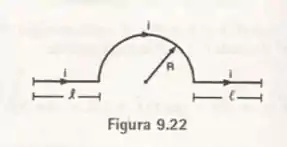
O fio mostrado na Figura conduz uma corrente . Determinar a intensidade do campo magnético no centro de do semicírculo, produzido:
b) pelo segmento semicircular de raio
Passo 1
Aqui, aplicando a lei de Biot-Savart, temos:
Já que a distância é sempre e o ângulo vai de por ser uma semicircunferência.
Calculando então:
E pronto, essa é a intensidade do campo produzido pelo segmento semicircular😉
Resposta
Exercícios de Livros Relacionados
Calcule a integral de linha, onde C é a curva dada. ∫ C yd s C : x = t 2 ,y = t ,0 ≤ t ≤ 2
29- Se C é a curva com equações paramétricas x = ln t , y = e - t , 1 ≤ t ≤ 2 , use uma calculadora ou CAS para calcular a integral de linha ∫ C xs e nyd s com precisão até a terceira casa decimal.
Calcular as integrais curvilíneas. ∫ C 2 x yd s , onde C é o arco de circunferência x 2 + y 2 = 4 de 2,0a1 ,3
Calcular as integrais curvilíneas. ∫ C y 2d s , onde C é o primeiro arco da cicloide: r - t = 2 t - s e nt i → + 2 ( 1 - cos t ) j -
Calcular as integrais curvilíneas. ∫ C x 2 d s , C é o arco da hipociclóide x 2 3 + y 2 3 = a 2 3 , a0 , primeiro quadrante.